
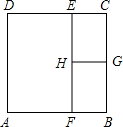
 如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )
如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )A、
| ||||
B、1+
| ||||
C、
| ||||
D、1+
|
科目:初中数学 来源: 题型:
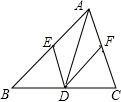 如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:
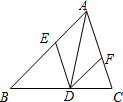 如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市九年级中考模拟(二)数学试卷(解析版) 题型:选择题
如图,已知扇形的圆心角为 (定值),半径为
(定值),半径为 (定值),分别在图一、二中
(定值),分别在图一、二中
作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩
,则按图二作出的矩
形面积的最大值为 ( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD和正方形EFGH的边长分别为2![]() 和
和![]() ,对角线BD,FH都在直线L上,O1,O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心矩.当中心O2在直线L上平移时,正方形EFGH也随着平移,在平移时正方形EFGH的形状,大小没有改变.
,对角线BD,FH都在直线L上,O1,O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心矩.当中心O2在直线L上平移时,正方形EFGH也随着平移,在平移时正方形EFGH的形状,大小没有改变.
(1)计算:O1D=_______,O2F=_______.
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=_____.
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
![]()
![]() 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 在第一象限内的图象经过点D、E,且 .
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 在第一象限内的图象经过点D、E,且 .
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩
| |
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com