
【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线![]() 过点A(—1,0),与⊙C相切于点D,
过点A(—1,0),与⊙C相切于点D,
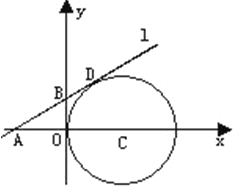
(1)求∠CAD的度数。
(2)求直线![]() 的解析式。
的解析式。
【答案】(1)30°(2)y=![]() x+
x+![]()
【解析】
试题分析:(1)连接CD,由于直线l为⊙C的切线,故CD⊥AD.C点坐标为(1,0),故OC=1,即⊙C的半径为1,由点A的坐标为(-1,0),可求出∠CAD=30度.作DE⊥AC于E点,则∠CDE=∠CAD=30°;(2)可求出CE=![]() ,点B的坐标为(0,
,点B的坐标为(0, ![]() ).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
试题解析:(1)连接CD,∵直线![]() 为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
又∵点A的坐标为(-1,0),∴AC=2,∴∠CAD=30°。
(2)作DE⊥AC于E点,则∠CDE=∠CAD=30°,∴CE=![]() ,
,
![]() ,∴OE=OC-CE=
,∴OE=OC-CE=![]() ,∴点D的坐标为(
,∴点D的坐标为(![]() ,
,![]() )。
)。
设直线![]() 的函数解析式为
的函数解析式为![]() ,则
,则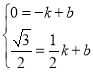
解得k=![]() ,b=
,b=![]() ,
,
∴直线![]() 的函数解析式为y=
的函数解析式为y=![]() x+
x+![]()


科目:初中数学 来源: 题型:
【题目】某饮料瓶上有这样的字样:Eatable Date 18 months.如果用x(单位:月)表示Eatable Date(保质期),那么该饮料的保质期可以用不等式表示为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).
(1)确定此一次函数的解析式.
(2)求坐标原点O到直线AB的距离.
(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com