
【题目】如图,在![]() 中,
中,![]() ,按以下步骤作图:
,按以下步骤作图:
①:以点![]() 为圆心,以小于
为圆心,以小于![]() 的长为半径画弧,分别交
的长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
②:分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ;
;
③:作射线![]() ,交
,交![]() 边于点
边于点![]() ,
,
若![]() ,
,![]() ,则
,则![]() ( )
( )
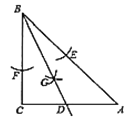
A. 3B. ![]() C. 6D.
C. 6D. ![]()
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
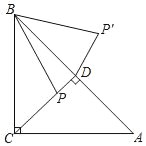
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
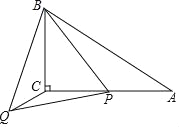
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明准备测量学校旗杆AB的高度,他发现阳光下,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成锐角为26°,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
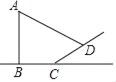
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,菱形![]() 与菱形
与菱形![]() 的顶点
的顶点![]() 重合,点
重合,点![]() 在对角线
在对角线![]() 上,且
上,且![]() .
.
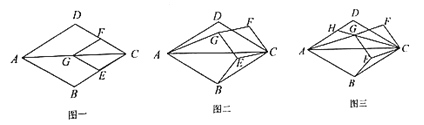
(1)问题发现:
![]() 的值为________;
的值为________;
(2)探究与证明:
将菱形![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 角(
角(![]() ),如图二所示,试探究线段
),如图二所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)拓展与运用:
菱形![]() 在旋转过程中,当点
在旋转过程中,当点![]() ,
,![]() ,
,![]() 三点在一条直线上时,如图三所示,连接
三点在一条直线上时,如图三所示,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
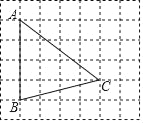
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交于(0,3)点.
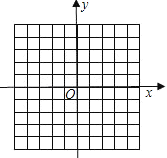
(1)求出m的值并画出这条抛物线;
(2)求它与x轴的交点和抛物线顶点的坐标;
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,点D、E分别在边AC、AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )

A. AE=AD;B. BD=CE;C. ∠ECB=∠DBC ;D. ∠BEC=∠CDB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com