
已知梯形 中,
中,
 于
于

 于
于
 相交于
相交于 的中点
的中点
(1)若点 为线段
为线段 上一点,且
上一点,且 过
过 点作
点作 于
于 试证:
试证:
(2)求证:
(1)∵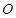 为
为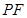 中点,
中点,
∴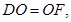
又∵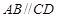 且
且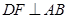
∴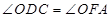
∴在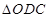 和
和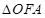 中,
中,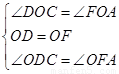
∴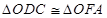 ······································
3分
······································
3分
∴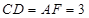
又∵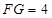
∴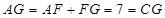
即: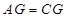 ··········································4分
··········································4分
又∵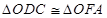
∴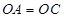
连接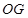
∵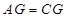
∴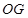 为
为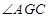 的角平分线
的角平分线
∵
∴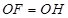 ·················································5分
·················································5分
(2)过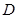 作
作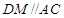 交
交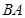 的延长线于
的延长线于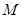
∵梯形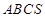 中,
中,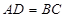
∴
又∵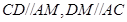
∴四边形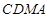 为
为 ,
,
∴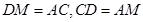 ·················6分
·················6分
∵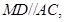 又
又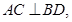 且
且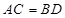
∴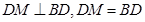
∴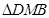 为等腰直角三角形
为等腰直角三角形
又∵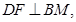 ∴
∴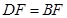
∴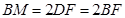
∴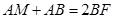 ·············································7分
·············································7分
∵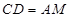
∴
∵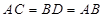
∴在 和
和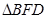 中
中
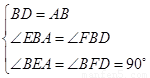
∴ ···············································9分
···············································9分
∴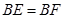
∵
∴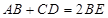 ···············································10分
···············································10分
【解析】略


科目:初中数学 来源: 题型:
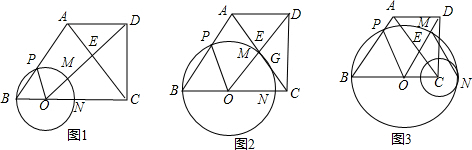
| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
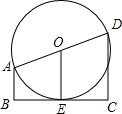 已知,直角梯形ABCD中,较短底AB=a,较长底DC=c,垂直于底的腰BC=b,以另一腰AD为直径作⊙O.
已知,直角梯形ABCD中,较短底AB=a,较长底DC=c,垂直于底的腰BC=b,以另一腰AD为直径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .点O为线段BC上的动点,连接OD,以O为圆心,OB为半径的⊙O分别交线段AB、OD于点P、M,交射线BC于点N,连接AC、MN,AC交线段OD于点E.
.点O为线段BC上的动点,连接OD,以O为圆心,OB为半径的⊙O分别交线段AB、OD于点P、M,交射线BC于点N,连接AC、MN,AC交线段OD于点E.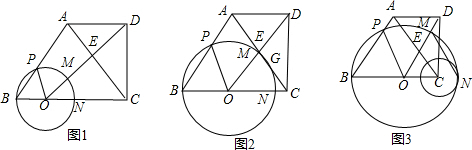
查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题



查看答案和解析>>
科目:初中数学 来源:2010年江苏省扬州市高邮市九年级第二次网络阅卷适应性数学试卷(解析版) 题型:解答题
 .点O为线段BC上的动点,连接OD,以O为圆心,OB为半径的⊙O分别交线段AB、OD于点P、M,交射线BC于点N,连接AC、MN,AC交线段OD于点E.
.点O为线段BC上的动点,连接OD,以O为圆心,OB为半径的⊙O分别交线段AB、OD于点P、M,交射线BC于点N,连接AC、MN,AC交线段OD于点E.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com