
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D,E分别是边
,点D,E分别是边![]() ,
,![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点C按逆时针方向旋转,记旋转角为α.
绕点C按逆时针方向旋转,记旋转角为α.
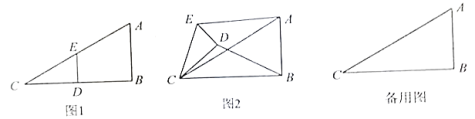
(1)问题发现
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;
;
(2)拓展探究
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
当![]() 旋转至
旋转至![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() ;(2)不变,证明见解析;(3)2
;(2)不变,证明见解析;(3)2![]() 或2
或2![]()
【解析】
(1)①当![]() =0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出BD、AE的比值;
=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出BD、AE的比值;
②中,图形如下,与①有所变化,但求解方法完全相同;
(2)证明△ECA∽△DCB,从而根据边长成比例得出比值;
(3)存在2种情况,一种是当![]() 时,
时,![]() ;另一种是当
;另一种是当![]() 时,
时,![]() ,分别利用勾股定理可求得.
,分别利用勾股定理可求得.
(1)①∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D,E分别是边
,点D,E分别是边![]() ,
,![]() 的中点
的中点
∴CD=BD=2,在Rt△ABC中,AB=![]() ,AC=
,AC=![]()
∴AE=![]()
∴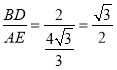 ;
;
②图形如下:
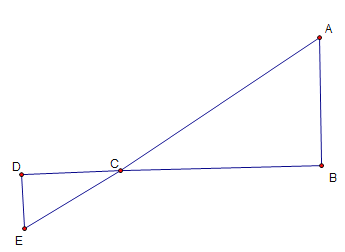
同理可知:BC=4,AC=![]() ,DC=2,DE=
,DC=2,DE=![]() ,CE=
,CE=![]()
∴BD=DC+CB=2+4=6,AE=EC+AC=![]() =
=![]()
∴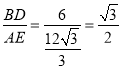 ;
;
(2)不变,理由如下
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() ,
,
∴△ECA∽△DCB,
∴![]() ;
;
(3)情况一:当![]() 时,
时,![]() ,图形如下,过点D作BC的垂线,交BC延长线于点F
,图形如下,过点D作BC的垂线,交BC延长线于点F
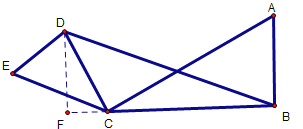
∵ED∥AC,∴∠ACD=∠EDC=90°
∵∠ACB=∠ECD=30°
∴∠ECF=30°,∴∠FCD=60°
∵CD=2
∴在Rt△DCF中,CF=1,FD=![]()
∴FB=FC=CB=1+4=5
∴在Rt△FDB中,DB=![]() 2
2![]() ;
;
情况二:当![]() 时,
时,![]() ,图形如下,过点D作BC的垂线,交BC于点F
,图形如下,过点D作BC的垂线,交BC于点F
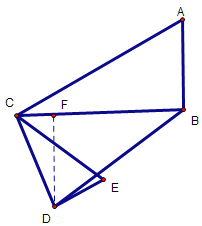
∵DE∥AC,∴∠ACD=90°
∵∠ACB=30°,∴∠DCF=60°
∵CD=2,∴在Rt△CDF中,CF=1,DF=![]()
∴FB=CB-CF=4-1=3
∴在Rt△FDB中,DB=![]() 2
2![]()
综上得:DB的长为2![]() 或2
或2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的一条弦,点
的一条弦,点![]() 在
在![]() 上,联结
上,联结![]() 并延长,交弦
并延长,交弦![]() 于点
于点![]() ,且
,且![]() .
.
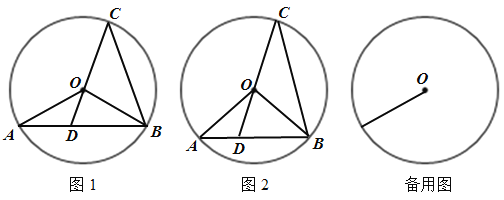
(1)如图1,如果![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,如果![]() ,求
,求![]() 的值;
的值;
(3)延长线段![]() 交弦
交弦![]() 于点
于点![]() ,如果
,如果![]() 是等腰三角形,且
是等腰三角形,且![]() 的半径长等于
的半径长等于![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学号召全校学生进行安全教育网络学习,并对部分学生的学习情况进行了随机调查.对部分学生的成绩(x为整数,满分100分)进行统计,并绘制了如下统计图表.
调查结果频数分布表
| 调查结果扇形统计图
|
根据所给信息,解答下列问题:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形统计图中,m的值及A组对应的圆心角的度数;
(3)若参加学习的同学共有1500人,请你估计成绩不低于80分的同学有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
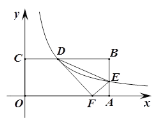
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=![]() (k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖市某医院计划选购A,B两种防护服.已知A防护服每件价格是B防护服每件价格的2倍,用80000元单独购买A防护服比用80000元单独购买B防护服要少50件.如果该医院计划购买B防护服的件数比购买A防护服件数的2倍多8件,且用于购买A,B两种防护服的总经费不超过320000元,那么该医院最多可以购买多少件B防护服?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com