
����Ŀ��ij���г���Ӫ������![]() �ͣ�
�ͣ�![]() ������Ʒ�����г���������������ۼ۸����±���(����1�������г����ۼ�����۱��ֲ���)
������Ʒ�����г���������������ۼ۸����±���(����1�������г����ۼ�����۱��ֲ���)
|
| |
�����۸�(Ԫ/��) | 1000 | 1100 |
���ۼ۸�(Ԫ/��) |
| 1500 |
���꾭������������![]() �ͳ�ÿ�����ۼ۱�ȥ������400Ԫ����֪
�ͳ�ÿ�����ۼ۱�ȥ������400Ԫ����֪![]() �ͳ�ȥ��1�·������ܶ�Ϊ3.6��Ԫ������1�·�
�ͳ�ȥ��1�·������ܶ�Ϊ3.6��Ԫ������1�·�![]() �ͳ�������������ȥ��1�·���ͬ���������ܶ��ȥ��1�·�����
�ͳ�������������ȥ��1�·���ͬ���������ܶ��ȥ��1�·�����![]() ��
��
��1���������1�·ݵ�![]() �����г��ۼ�Ϊ
�����г��ۼ�Ϊ![]() Ԫ/������
Ԫ/������![]() ��ֵ��(���з��̵ķ������)
��ֵ��(���з��̵ķ������)
��2���õ�ƻ�8�·��ٽ�һ��![]() �ͺ�
�ͺ�![]() �����г���50������
�����г���50������![]() �ͳ�����������
�ͳ�����������![]() �ͳ�������2����Ӧ��ν�������ʹ�������г�������ࣿ
�ͳ�������2����Ӧ��ν�������ʹ�������г�������ࣿ
��3���õ�Ϊ������Դ��������һ�ֽ���Ϊ500Ԫ��![]() �ͳ���Ԥ����8��Ԫ���������ֳ�������������
�ͳ���Ԥ����8��Ԫ���������ֳ�������������![]() ����
����![]() �͵�����֮��Ϊ
�͵�����֮��Ϊ![]() ����õ����ٿ��Թ������ֳ�����������
����õ����ٿ��Թ������ֳ�����������
���𰸡���1������1�·ݵ�![]() �����г��ۼ�Ϊ1200Ԫ����2��
�����г��ۼ�Ϊ1200Ԫ����2��![]() �ͽ�17����
�ͽ�17����![]() �ͽ�33��ʱ������ࣻ��3���õ����ٿ��Թ�����92����
�ͽ�33��ʱ������ࣻ��3���õ����ٿ��Թ�����92����
��������
��1�������1�·ݵ�![]() �����г��ۼ�Ϊ
�����г��ۼ�Ϊ![]() Ԫ�����������г����̣���⼴�ɣ�
Ԫ�����������г����̣���⼴�ɣ�
��2���蹺��![]() �����г�
�����г�![]() ��������
��������![]() �ͳ�����������
�ͳ�����������![]() �ͳ�������2���г�����ʽ���a�ķ�Χ�����г�W��a�Ĺ�ϵʽ���ݴ����W�����ֵ���ɣ�
�ͳ�������2���г�����ʽ���a�ķ�Χ�����г�W��a�Ĺ�ϵʽ���ݴ����W�����ֵ���ɣ�
��3���蹺��![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() �����г�n��a�ķ��̣����
�����г�n��a�ķ��̣����![]() ���õ���
���õ���![]() ʱ��
ʱ��![]() ��СֵΪ92.
��СֵΪ92.
�⣺��1�������1�·ݵ�![]() �����г��ۼ�Ϊ
�����г��ۼ�Ϊ![]() Ԫ��
Ԫ��
��ȥ��![]() �����г��ۼ�Ϊ
�����г��ۼ�Ϊ![]() Ԫ��
Ԫ��
�������⣬��![]() ��
��
��ã�![]() ��
��
�����飬![]() �����з�ʽ���̵Ľ⣬
�����з�ʽ���̵Ľ⣬
�����1�·ݵ�![]() �����г��ۼ�Ϊ1200Ԫ��
�����г��ۼ�Ϊ1200Ԫ��
��2���蹺��![]() �����г�
�����г�![]() ������
������![]() �����г�
�����г�![]() ����
����
![]()
��ã�![]() ����
����![]() ����
����
��������![]()
��Ϊ![]() ������
������![]() ��
��![]() �����������
�����������
�൱![]() ʱ����
ʱ����![]() �ͽ�17����
�ͽ�17����![]() �ͽ�33��ʱ������࣮
�ͽ�33��ʱ������࣮
��3���蹺��![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
�������⣬�ã�![]()
��ã�![]() ��
��
��Ϊ![]() ������
������![]() ����
����![]() ������
������
��Ϊ![]() Ϊ����������
Ϊ����������![]() Ϊ5�ı�����
Ϊ5�ı�����
�൱![]() ʱ��
ʱ��![]() ��СֵΪ92��
��СֵΪ92��
�𣺸õ����ٿ��Թ�����92��.


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() ��
��![]() �ᡢ
�ᡢ![]() �ύ��
�ύ��![]() ��
��![]() ���㣬�뷴��������
���㣬�뷴��������![]()
![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ��
��
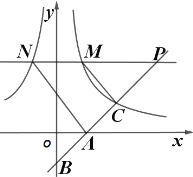
��1�����������Ľ���ʽ��
��2����![]()
![]() ��ֱ��
��ֱ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ���ƽ���߽�����������
���ƽ���߽�����������![]()
![]() ��
��![]()
![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬��
��һ�㣬��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ������
������![]() ��
��
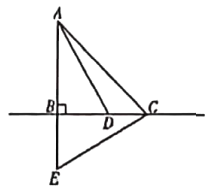
![]() ��֤:
��֤:![]() ��
��
![]() ��
��![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
![]() ��
��![]() ��
��![]() �����ģ�����
�����ģ�����![]() ��ֱ��
��ֱ��![]() ���˶����ҵ�
���˶����ҵ�![]() ǡ����
ǡ����![]() �ڲ������ʱ��ֱ��д����
�ڲ������ʱ��ֱ��д����![]() �˶���·���ij���
�˶���·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
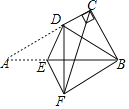
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() �DZ�
�DZ�![]() ��һ����(����
��һ����(����![]() ��
��![]() �غ�)����
�غ�)����![]() ���ڵ�ֱ���۵�
���ڵ�ֱ���۵�![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() ��ֱ����������
��ֱ����������![]() Ϊֱ�DZ�ʱ����
Ϊֱ�DZ�ʱ����![]() �ij�Ϊ____��
�ij�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
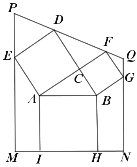
����Ŀ�����ɶ��������ƾõ���ʷ����������ܶ��˵���Ȥ��1955��ϣ����������ö�Թ���ͼΪ��������Ʊ����ν����ͼ��ָ��ֱ�������ε�����Ϊ�������������ι��ɣ���������֤���ɶ�������ͼ�Ĺ���ͼ�У���֪![]() ��
��![]() ��
��![]() .���ı���
.���ı���![]() �������
�������![]() ��
��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �Ľ��㣮��ô
�Ľ��㣮��ô![]() �ij�����(����)
�ij�����(����)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ɻ��ڿ���̽��ij��ɽ�ĸ߶ȣ��ڵ�A���ɻ��ķ��и߶���AF��3700�ף��ӷɻ��Ϲ۲�ɽ��Ŀ��C�ĸ�����45�����ɻ���������ͬ�ĸ߶ȷ���300��B������ʱ�۲�Ŀ��C�ĸ�����50�������ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.20��
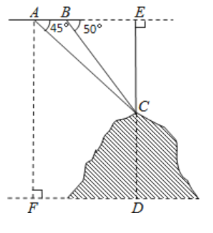
��1��ֱ��д����ACB�Ĵ�С��
��2��������ɽ�ĸ߶�CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
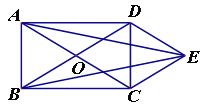
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��DE��AC��CE��BD.
��1����֤���ı���OCEDΪ���Σ�
��2������AE��BE��AE��BE�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
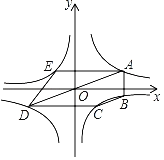
����Ŀ����ͼ������ԭ��O��ֱ���뷴��������y��![]() ��a��0����ͼ����A��D���㣨��A�ڵ�һ���ޣ�����B��C��E�ڷ���������y��
��a��0����ͼ����A��D���㣨��A�ڵ�һ���ޣ�����B��C��E�ڷ���������y��![]() ��b��0����ͼ���ϣ�AB��y�ᣬAE��CD��x�ᣬ�����ABCDE�����Ϊ56���ı���ABCD�����Ϊ32����a��b��ֵΪ__��
��b��0����ͼ���ϣ�AB��y�ᣬAE��CD��x�ᣬ�����ABCDE�����Ϊ56���ı���ABCD�����Ϊ32����a��b��ֵΪ__��![]() ��ֵΪ__��
��ֵΪ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���Ż�����������ijһС�����������̻������мס��������̻���˾������Ͷ�꣬�����Ƴ����̻��շѷ������£���˾�̻�����![]() ��Ԫ�� ���̻����
��Ԫ�� ���̻����![]() ��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ��
��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ��
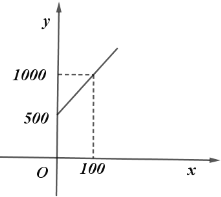
�ҹ�˾���̻����������1000ƽ����ʱ��ͳһ��ȡ����5000Ԫ���̻��������1000ƽ����ʱ����������ÿƽ������ȡ3Ԫ��
��1����ס��ҹ�˾�̻�����![]() ��Ԫ�����̻����
��Ԫ�����̻����![]() ��ƽ���ף��ĺ�������ʽ��
��ƽ���ף��ĺ�������ʽ��
��2�������С��Ŀǰ���̻������1500ƽ���ף���ͨ������˵����ѡ���ļҹ�˾���̻����ý��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com