
分析 (1)根据完全平方公式和平方差公式先将代数式进行变形,然后利用三角形三边关系即可判断.
(2)根据完全平方公式将题目所给的等式进行变形,然后利用非负性即可求出答案.
解答 解:(1)a2-2ab-c2+b2=(a-b)2-c2=(a-b+c)(a-b-c)
∵a+c>b,a<b+c,
∴a-b+c>0,a-b-c<0,
∴a2-2ab-c2+b2<0
(2)∵a2+b2+c2=ab+ac+bc
∴2a2+2b2+2c2-2ab-2ac-2bc=0,
∴a2-2ab+b2+b2-2bc+c2+a2-2ac+c2=0,
∴(a-b)2+(b-c)2+(a-c)2=0,
∴a-b=0,b-c=0,a-c=0,
∴a=b=c,
∴△ABC是等边三角形.
点评 本题考查三角形三边关系,涉及等边三角形的判定,任意三角形三边关系,完全平方公式,题目较为综合.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
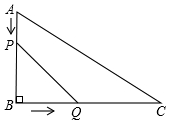 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
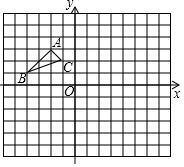 如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).
如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com