
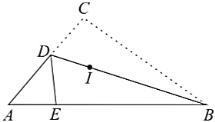
【题目】如图,三角形纸片![]() 中,沿过
中,沿过![]() 点的直线折叠这个三角形,使点
点的直线折叠这个三角形,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,则下列结论:
,则下列结论:
①![]() 平分
平分![]() ;
;
②![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为7;
的周长为7;
④![]() ;
;
⑤若![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,
时,![]() .其中结论正确的有( )
.其中结论正确的有( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
根据折叠的性质,可知∠BDC=∠BED,BC=BE,DE=DC,可判断①③正确,再由三角形的面积计算公式可判断④正确,再根据角平分线的性质及三角形的内角和定理可判断⑤正确.用逆推的方法可判断②错误,从而得到正确的结果.
解:∵三角形纸片![]() 中,沿过
中,沿过![]() 点的直线折叠这个三角形,使点
点的直线折叠这个三角形,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,
,
∴∠BDC=∠BED,∠ABD=∠CBD,∠BED=∠C,BC=BE,DE=DC,
∴![]() 平分
平分![]() ;
;
故①正确;
假设![]() ,则
,则
∵∠ADE+∠CDE=180°,![]() ;
;
∴∠ABC+∠CDE=180°,
∵∠ABC+∠CDE+∠BED+∠C =360°,
∴∠BED+∠C =180°,
∵∠BED=∠C,
∴∠BED=∠C=90°,
而题中并没有已知∠C=90°,故假设不成立.
故②错误;
∵![]() ,
,![]() ,
,
∴AE=AB-BE=AB-BC=8-6=2.
∵AD+DE=AD+DC=AC=5.
∴![]() 的周长=AE+AD+DE=2+5=7;
的周长=AE+AD+DE=2+5=7;
故③正确;
如图,过点D作DF⊥AB于F,则
∵![]() ,
, ![]()
∴![]()
∵BC=BE,
∴![]()
∵![]()
∴![]() ;
;
故④正确;

∵![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() ,∠ABD=∠CBD,
,∠ABD=∠CBD,
∴∠BCI+∠CBI=![]() =
=![]()
∵![]() ,
,![]()
∴![]() .
.
∴∠BCI+∠CBI=65°,
∵∠BCI+∠CBI+∠BIC=180°,
∴∠BIC=115°,
故⑤正确;
综上所述,①③④⑤正确,故正确的个数有4个.
故选C.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
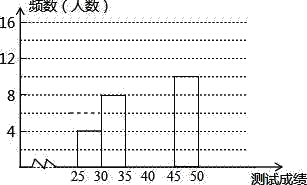
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
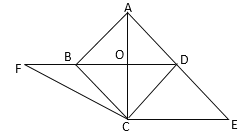
(1)求证:四边形BCED是平行四边形;
(2)延长DB至点F,联结CF,若CF=BD,求∠BCF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转一定角度(小于360°)得到△B′AC′.
(1)若点B′落在线段AC上,在图中画出△B′AC′,并直接写出当AC=4时,CC′的值;
(2)若∠ACB=20°,旋转后,B′C′⊥AC,请直接写出旋转角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品专卖店计划购进甲、乙两种不同类型的木雕工艺品,已知![]() 件甲种工艺品的进价与
件甲种工艺品的进价与![]() 件乙种工艺品的进价的和为
件乙种工艺品的进价的和为![]() 元,
元,![]() 件甲种工艺品的进价与
件甲种工艺品的进价与![]() 件乙种工艺品的进价的和为
件乙种工艺品的进价的和为![]() 元.
元.

(1)求每件甲种、乙种工艺品的进价分别是多少元;
(2)如果购进甲种工艺品有优惠,优惠方法是:购进甲种工艺品超过![]() 件,超出部分可以享受
件,超出部分可以享受![]() 折优惠.若购进
折优惠.若购进![]() (
(![]() 为正整数)件甲种工艺品需要花费
为正整数)件甲种工艺品需要花费![]() 元,请你写出
元,请你写出![]() 与
与![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
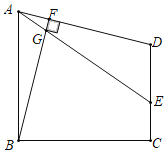
【题目】在四边形ABCD中,∠ABC=∠DCB=90°,AB=BC.过点B作BF⊥AD,垂足为点F,
(1)求证:∠DAB=∠FBC;
(2)点E为线段CD上的一点,连接AE交BF于G,若∠BAE+2∠EAD=90°,AG=1,AB=5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
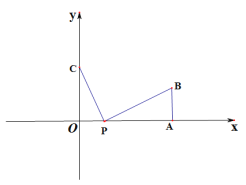
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
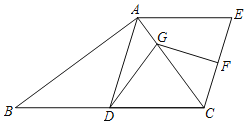
【题目】如图,在Rt△ABC中,AD为斜边BC上的中线,AE∥BC,CE∥AD,EC的垂直平分线FG交AC点G,连接DG,若∠ADG=24°,则∠B的度数为_____度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com