
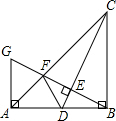
 ��ͼ����Rt��ABC�У���ABC=90�㣬BA=BC����D��AB���е㣬����CD������B��BG��CD���ֱ�CD��CA�ڵ�E��F�������A�Ҵ�ֱ��AB��ֱ���ཻ�ڵ�G������DF�����������ĸ����ۣ���$\frac{AG}{AB}=\frac{FG}{FB}$����FG=$\frac{1}{2}$FB����AF=$\frac{\sqrt{2}}{3}AB$����S��ABC=5S��BDF��������ȷ���۵�����Ǣ٢ڢۣ�
��ͼ����Rt��ABC�У���ABC=90�㣬BA=BC����D��AB���е㣬����CD������B��BG��CD���ֱ�CD��CA�ڵ�E��F�������A�Ҵ�ֱ��AB��ֱ���ཻ�ڵ�G������DF�����������ĸ����ۣ���$\frac{AG}{AB}=\frac{FG}{FB}$����FG=$\frac{1}{2}$FB����AF=$\frac{\sqrt{2}}{3}AB$����S��ABC=5S��BDF��������ȷ���۵�����Ǣ٢ڢۣ� ���� ����ͬ�ǵ������������ABG=��BCD��Ȼ�����á��DZ߽ǡ�֤����ABC�͡�BCDȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AG=BD��Ȼ�����AG=$\frac{1}{2}$BC���������AFG�͡�CFB���ƣ��������������ζ�Ӧ�߳ɱ����ɵ�$\frac{AG}{AB}$=$\frac{FG}{FB}$���Ӷ��жϳ�����ȷ����AG=$\frac{1}{2}$BC������FG=$\frac{1}{2}$FB���ʢ���ȷ���������������ζ�Ӧ�߳ɱ������$\frac{AF}{FC}$=$\frac{1}{2}$���ٸ��ݵ���ֱ�������ε����ʿɵ�AC=$\sqrt{2}$AB��Ȼ���������ɵõ�AF=$\frac{\sqrt{2}}{3}$AB���жϳ�����ȷ������F��MF��AB��M�����������ε�������������жϳ��ܴ���
��� �⣺�ߡ�ABC=90�㣬BG��CD��
���ABG+��CBG=90�㣬��BCD+��CBG=90�㣬
���ABG=��BCD��
�ڡ�ABC�͡�BCD�У�
$\left\{\begin{array}{l}{��ABG=��BCD}\\{AB=BC}\\{��BAG=��CBD=90��}\end{array}\right.$��
���ABG�ա�BCD��ASA����
��AG=BD��
�ߵ�D��AB���е㣬
��BD=$\frac{1}{2}$AB��
��AG=$\frac{1}{2}$BC��
��Rt��ABC�У���ABC=90�㣬
��AB��BC��
��AG��AB��
��AG��BC��
���AFG�ס�CFB��
��$\frac{AG}{CB}=\frac{FG}{FB}$��
��BA=BC��
��$\frac{AG}{AB}=\frac{FG}{FB}$��
�ʢ���ȷ��
�ߡ�AFG�ס�CFB��
��$\frac{GF}{BF}=\frac{AG}{BC}=\frac{1}{2}$��
��FG=$\frac{1}{2}$FB��
�ʢ���ȷ��
�ߡ�AFG�ס�CFB��
��$\frac{AF}{CF}=\frac{AG}{AC}=\frac{1}{2}$��
��AF=$\frac{1}{3}$AC��
��AC=$\sqrt{2}$AB��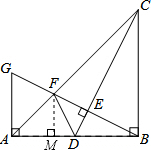 ��AF=$\frac{\sqrt{2}}{3}$AB���ʢ���ȷ��
��AF=$\frac{\sqrt{2}}{3}$AB���ʢ���ȷ��
����F��MF��AB��M����FM��CB��
��$\frac{AF}{AC}=\frac{FM}{BC}=\frac{1}{3}$��
��$\frac{BD}{BA}=\frac{1}{2}$��
��$\frac{S��BDF}{S��ABC}$=$\frac{\frac{1}{2}BD•FM}{\frac{1}{2}AB•BC}$=$\frac{BD}{AB}•\frac{FM}{BC}$=$\frac{1}{2}��\frac{1}{3}$=$\frac{1}{6}$���ʢܴ���
�ʴ�Ϊ���٢ڢۣ�
���� ���⿼�������������ε��ж������ʣ�ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ������������������ε��ж����������������ζ�Ӧ�߳ɱ����������ǽ���Ĺؼ���


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
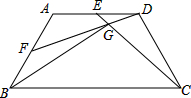 ��ͼ����֪��������ABCD�У�AD��BC����A=120�㣬AB=AD=CD����E����F�ֱ�Ϊ�߶�AD��AB���е㣬����CE��DF��CE��DF�ཻ�ڵ�G������BG����DG=2�����߶�BG�ij�Ϊ2$\sqrt{13}$��
��ͼ����֪��������ABCD�У�AD��BC����A=120�㣬AB=AD=CD����E����F�ֱ�Ϊ�߶�AD��AB���е㣬����CE��DF��CE��DF�ཻ�ڵ�G������BG����DG=2�����߶�BG�ij�Ϊ2$\sqrt{13}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
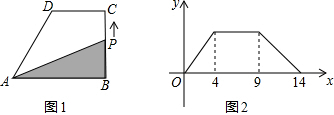
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
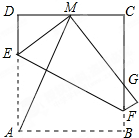 ���߳�Ϊ5������ABCD�۵���ʹ����A��CD���ϵĵ�M�غϣ��ۺ۽�AD��E����BC��F����AB�۵�����BC�߽��ڵ�G��
���߳�Ϊ5������ABCD�۵���ʹ����A��CD���ϵĵ�M�غϣ��ۺ۽�AD��E����BC��F����AB�۵�����BC�߽��ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
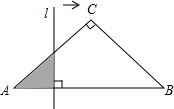 ��ͼ���ڡ�ABC�У�AC=BC����C=90�㣬ֱ��l��AB��ֱ��l�ӵ�A��ʼ����������ƽ���ƶ�����ֱ��l�ƶ���ʱ��Ϊt��ɨ����ABC�������ͼ����Ӱ���֣�ΪS�������и�ͼ�У��ܹ���ӳS����t�ĺ�����ϵ�Ĵ���ͼ���ǣ�������
��ͼ���ڡ�ABC�У�AC=BC����C=90�㣬ֱ��l��AB��ֱ��l�ӵ�A��ʼ����������ƽ���ƶ�����ֱ��l�ƶ���ʱ��Ϊt��ɨ����ABC�������ͼ����Ӱ���֣�ΪS�������и�ͼ�У��ܹ���ӳS����t�ĺ�����ϵ�Ĵ���ͼ���ǣ�������| A�� | 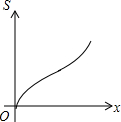 | B�� | 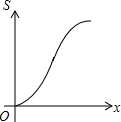 | C�� | 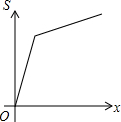 | D�� | 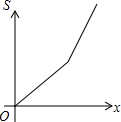 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A��B��C��DΪ��O�ϵ��ĵȷֵ㣬����P��Բ��O��������O-C-D-O��·���������˶������˶���ʱ��Ϊt�룬��APB�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ�������
��ͼ����A��B��C��DΪ��O�ϵ��ĵȷֵ㣬����P��Բ��O��������O-C-D-O��·���������˶������˶���ʱ��Ϊt�룬��APB�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ�������| A�� | 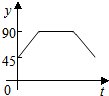 | B�� | 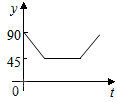 | C�� | 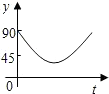 | D�� | 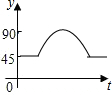 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
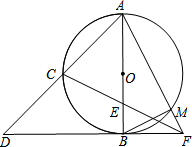 ��ͼ��AB�ǡ�O��ֱ����C��$\widehat{AB}$���е㣬�ӳ�AC����D��ʹAC=CD��DB���ӳ��߽�CE���ӳ����ڵ�F��AF����O�ڵ�M������BM��
��ͼ��AB�ǡ�O��ֱ����C��$\widehat{AB}$���е㣬�ӳ�AC����D��ʹAC=CD��DB���ӳ��߽�CE���ӳ����ڵ�F��AF����O�ڵ�M������BM���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com