
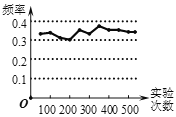
【题目】如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是_______(填序号).
①抛一枚质地均匀的硬币,落地时结果“正面朝上”;
②在“石头,剪刀,布”的游戏中,小明随机出的是剪刀;
③四张一样的卡片,分别标有数字1,2,3,4,从中随机
取出一张,数字是1.
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
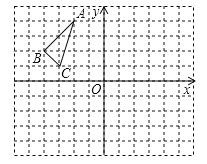
【题目】 ![]() 在平面直角坐标系中的位置如图,其中每个小正方形的边长为
在平面直角坐标系中的位置如图,其中每个小正方形的边长为![]() 个单位长度.
个单位长度.
![]() 画出
画出![]() 关于原点
关于原点![]() 的中心对称图形
的中心对称图形![]() ;
;
![]() 画出将
画出将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() .
.
![]() 在
在![]() 的条件下,求点
的条件下,求点![]() 旋转到点
旋转到点![]() 所经过的路线长(结果保留
所经过的路线长(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
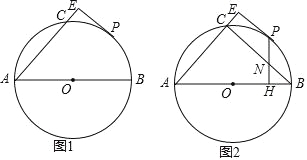
【题目】如图1,AB是⊙O的直径,AC是弦,点P是![]() 的中点,PE⊥AC交AC的延长线于E.
的中点,PE⊥AC交AC的延长线于E.
(1)求证:PE是⊙O的切线;
(2)如图2,作PH⊥AB于H,交BC于N,若NH=3,BH=4,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
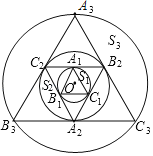
【题目】如图,小圆O的半径为1,△A1B1C1,△A2B2C2,△A3B3C3,…,△AnBnn依次为同心圆O的内接正三角形和外切正三角形,由弦A1C1和弧A1C1围成的弓形面积记为S1,由弦A2C2和弧A2C2围成的弓形面积记为S2,…,以此下去,由弦Ann和弧Ann围成的弓形面积记为Sn,其中S2020的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]()
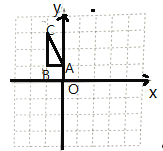
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)画出![]() 绕原点
绕原点![]() 顺时针方向旋转
顺时针方向旋转![]() 后得到的
后得到的![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(3)将![]() 平移得到
平移得到![]() ,使点
,使点![]() 的对应点是
的对应点是![]() ,点
,点![]() 的对应点时
的对应点时![]() ,点
,点![]() 的对应点是
的对应点是![]() ,在坐标系中画出
,在坐标系中画出![]() ,并写出点
,并写出点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
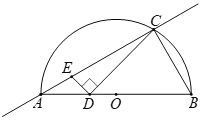
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
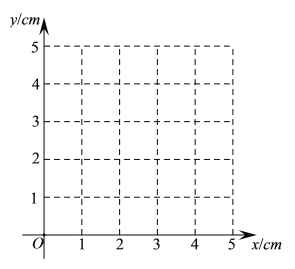
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(![]() )时,每月的销售量
)时,每月的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
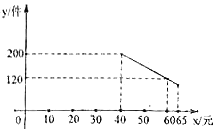
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设每月获得的利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若想每月获得1600元的利润,那么销售单价应定为多少元?
(4)当销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
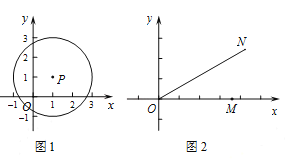
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
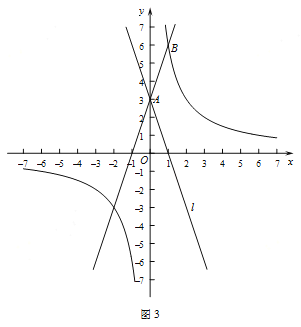
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com