
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
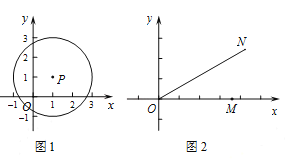
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
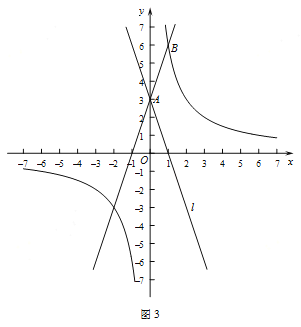
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
【答案】(1)解:![]() ,3(2)解:直线
,3(2)解:直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系是相切. (3)①点
倍相关圆的位置关系是相切. (3)①点![]() 的3倍相关圆的半径是3;②
的3倍相关圆的半径是3;②![]() 的最大值是
的最大值是![]() .
.
【解析】
(1)根据点![]() 的
的![]() 倍相关圆的定义即可判断出答案;
倍相关圆的定义即可判断出答案;
(2)设点![]() 的坐标为
的坐标为![]() ,求得点
,求得点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,再比较与点
,再比较与点![]() 到直线直线
到直线直线![]() 的距离即可判断;
的距离即可判断;
(3)①先求得直线![]() 的解析式,
的解析式,
(1)![]() 的1倍相关圆,半径为:
的1倍相关圆,半径为:![]() ,
,
![]() 的1倍相关圆,半径为:
的1倍相关圆,半径为:![]() ,不符合,
,不符合,
故答案为:![]() ,3;
,3;
(2)解:直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系是相切,
倍相关圆的位置关系是相切,
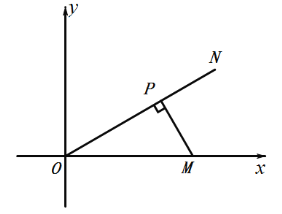
证明:设点![]() 的坐标为
的坐标为![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,
,
∴点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,
,
∴直线![]() 与点
与点![]() 的
的![]() 倍相关圆相切,
倍相关圆相切,
(3)①∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,
,
∴点B的坐标为:![]() ,
,
∵直线![]() 经过点
经过点![]() 和
和![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∵直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称,
轴对称,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
设点C的坐标为:![]() ,
,
∴点![]() 的3倍相关圆的半径是:
的3倍相关圆的半径是:![]() ,
,
故点![]() 的3倍相关圆的半径是3;
的3倍相关圆的半径是3;
②![]() 的最大值是
的最大值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
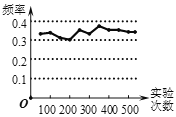
【题目】如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是_______(填序号).
①抛一枚质地均匀的硬币,落地时结果“正面朝上”;
②在“石头,剪刀,布”的游戏中,小明随机出的是剪刀;
③四张一样的卡片,分别标有数字1,2,3,4,从中随机
取出一张,数字是1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标为
图象的一部分,抛物线的顶点坐标为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,点
,点![]() 和点
和点![]() 均在直线
均在直线![]() 上.①
上.①![]() ;②
;②![]() ;③抛物线与
;③抛物线与![]() 轴的另一个交点时
轴的另一个交点时![]() ;④方程
;④方程![]() 有两个不相等的实数根;⑤
有两个不相等的实数根;⑤![]() ;⑥不等式
;⑥不等式![]() 的解集为
的解集为![]() .
.
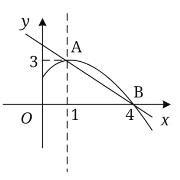
上述六个结论中,其中正确的结论是_____________.(填写序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
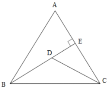
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种B.1种C.2种D.3种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
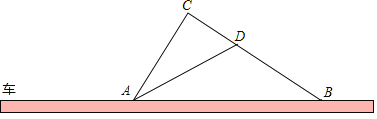
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于![]() FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )

A.12B.20C.24D.48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com