
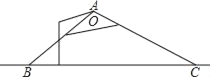
【题目】如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC=20米.
(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)
(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
【答案】(1)见解析;(2)是7.3米
【解析】
(1)图1,先以A为圆心,大于A到BC的距离为半径画弧交BC与EF两点,然后分别以E、F为圆心画弧,交点为G,连接AG,与BC交点点D,则AD⊥BC;图2,分别以B、C为圆心,BA为半径画弧,交于点G,连接AG,与BC交点点D,则AD⊥BC;(2)在△ABD中,DB=AD;在△ACD中,CD=![]() AD,BC=BD+CD,由此可以建立关于AD的方程,解方程求解.
AD,BC=BD+CD,由此可以建立关于AD的方程,解方程求解.
解:(1)如下图,
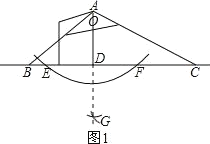
图1,先以A为圆心,大于A到BC的距离为半径画弧交BC与EF两点,然后分别以E、F为圆心画弧,交点为G,连接AG,与BC交点点D,则AD⊥BC;
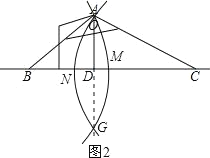
图2,分别以B、C为圆心,BA为半径画弧,交于点G,连接AG,与BC交点点D,则AD⊥BC;
(2)设AD=x,在Rt△ABD中,∠ABD=45°,
∴BD=AD=x,
∴CD=20﹣x.
∵tan∠ACD=![]() ,
,
即tan30°=![]() ,
,
∴x=![]() =10(
=10(![]() ﹣1)≈7.3(米).
﹣1)≈7.3(米).
答:路灯A离地面的高度AD约是7.3米.


科目:初中数学 来源: 题型:
【题目】某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:
的坐标定义如下:
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
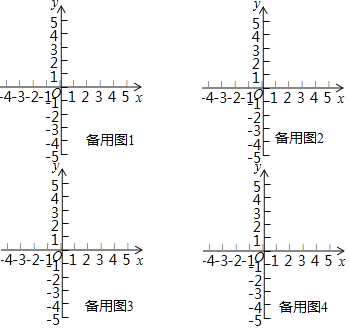
(1)点![]() 的变换点
的变换点![]() 的坐标是 ;点
的坐标是 ;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,则
,则![]() °;
°;
(2)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线上,点
![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值;
的值;
(3)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,以
,以![]() 为直径作
为直径作![]() ,
,![]() 的半径为
的半径为![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,∠BAC的平分线交BD于E,交BC于F,BH⊥AF于H,交AC于G,交CD于P,连接GE、GF,以下结论:①△OAE≌△OBG;②四边形BEGF是菱形;③BE=CG;④![]() ﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
﹣1;⑤S△PBC:S△AFC=1:2,其中正确的有( )个.
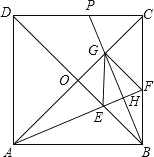
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学活动小组测量吉林市“世纪之舟”的高度.他们制定了测量方案,并利用课余时间完成了实地测景,测量项目及数据如下表:
项目 | 内容 | |||
课题 | 测量吉林市“实际之舟”的高度 | |||
示意图 |
| 如图,用测角仪在 | ||
测量数据 |
|
|
| 测角仪 |
|
| 50米 | 1.5米 | |
… | … | |||
请你根据活动小组测得的数据,求世纪之舟的高![]() (结果保留小数点后一位).
(结果保留小数点后一位).
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(![]() )求m的取值范围;
)求m的取值范围;
(![]() )若m取满足条件的最小的整数,
)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=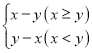 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
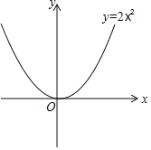
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)该函数的自变量![]() 的取值范围是______;
的取值范围是______;
(2)同学们先找到![]() 与
与![]() 的几组对应值,然后在下图的平面直角坐标系
的几组对应值,然后在下图的平面直角坐标系![]() 中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质:_______________.
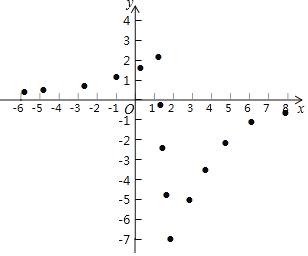
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com