
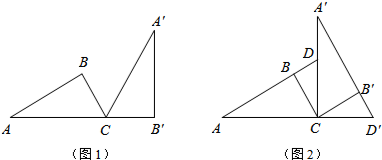
分析 (1)①由旋转的性质可知∠BCB′=120°,然后由扇形的弧长公式即可求得点B旋转经过的路径长;②由特殊锐角三角函数值可求得BB′的长;
(2)首先画出图形,然后根据S1=S2,可求得S1+S4的面积,然后再利用扇形面积-等边三角形ECD′的面积,从而可求得答案.
解答 解:(1)①∵AC=2,∠B=90°,∠A=30°,
∴BC=1.
∴点B旋转的路径=$\frac{1}{3}×2π×{1}^{2}$=$\frac{2}{3}$π;…(2分)
②如下图所示: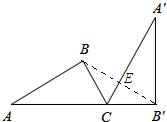
在△BCB′中,CB=CB′,∠BCB′=120°,AC⊥BB′
∴sin∠CBE=$\frac{BE}{BC}$=$\frac{\sqrt{3}}{2}$.
∴BE=$\frac{\sqrt{3}}{2}$.
∴BB′=$\sqrt{3}$;…(4分)
(2)如图所示: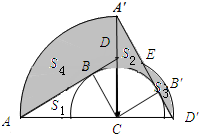 …(5分)
…(5分)
∵S1=S2,
∴S2+S4=S1+S4=$\frac{1}{4}$π(AC2-BC2)=$\frac{1}{4}π({2}^{2}-{1}^{2})$=$\frac{3}{4}π$.
在Rt△ABD中,DC=AC•tan30°=$\frac{2\sqrt{3}}{3}$,
S3=$\frac{1}{6}×π×(\frac{2\sqrt{3}}{3})^{2}$-$\frac{1}{2}×\frac{2\sqrt{3}}{3}×1$=$\frac{2}{9}π-\frac{\sqrt{3}}{3}$,
∴S2+S3+S4=$\frac{3}{4}π+\frac{2}{9}π-\frac{\sqrt{3}}{3}$=$\frac{35}{36}π-\frac{\sqrt{3}}{3}$.…(8分)
点评 本题主要考查的是旋转的性质,根据旋转的性质画出图形,然后根据S1=S2,求得S2+S4是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
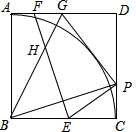 点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)
点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
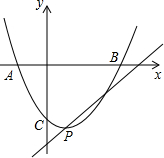 已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).
已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2y)(x-8y) | B. | (x+y)(x-16y) | C. | (-4y+x)(4y+x) | D. | (-x-4y)(x+4y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{-25}$ | B. | $\sqrt{-3}$ | C. | $\sqrt{(-9)^{2}}$ | D. | $\sqrt{-\frac{1}{1{0}^{2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com