
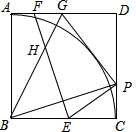
 点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)
点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号) 分析 先作NF⊥BC于N,根据正方形的性质和垂直平分线的性质证明△BCP≌△FNE就可以得出BP=EF,作BM⊥PG于M,GP⊥EP,通过证明两次三角形全等就可以得出∠PBG=45°,从而求出∠FHG=45°,由切线的判定定理就可以求出以BA为半径⊙B与GP相切,当G为AD的中点时,设AG=GD=x,CP=y,则GM=x,PM=y,PD=2x-y,运用勾股定理就可以求出DP与CP的关系.
解答 解:作NF⊥BC于N,
∴∠FNE=90°.
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠ADC=∠BAD=90°,AB=BC=CD=DA.
∴NF=AB
∴NF=CB.
∵EF垂直平分BP,
∴∠2=∠3,∠2+∠NEF=90°.
∵∠1+∠NEF=90°,
∴∠1=∠2,
在△BCP和△FNE中,
$\left\{\begin{array}{l}{∠2=∠1}\\{BC=FN}\\{∠C=∠FNE}\end{array}\right.$,
∴△BCP≌△FNE(ASA),
∴BP=EF;故①正确;
作BM⊥PG于M,GP⊥EP,
∴BM∥EP,∠BMP=∠BMG=90°
∴∠3=∠5,∠BMP=∠C.
∴∠2=∠5
在△BPC和△BPM中,
$\left\{\begin{array}{l}{∠C=∠BMP}\\{∠2=∠5}\\{BP=BP}\end{array}\right.$,
∴△BPC≌△BPM(AAS),
∴BC=AB=BM,
∴以BA为半径⊙B与GP相切.故②正确;
在Rt△BMG和Rt△BAG中,
$\left\{\begin{array}{l}{BG=BG}\\{BM=AB}\end{array}\right.$,
∴Rt△BMG≌Rt△BAG(HL),
∴∠6=∠7.
∵∠2+∠5+∠6+∠7=90°,
∴2∠5+2∠6=90°,
∴∠5+∠6=45°
即∠PBG=45°.
∴∠8=45°.
∴∠FHG=45°故③正确;
当G为AD的中点时,设AG=GD=x,CP=y,则GM=x,PM=y,PD=2x-y,
在Rt△PGD中由勾股定理,得
(x+y)2=x2+(2x-y)2,
∴y=$\frac{2}{3}$x,
即CP=$\frac{2}{3}$x
∴PD=2x-$\frac{2}{3}$x=$\frac{4}{3}$x,
∴DP=2CP故④正确.
∴正确的有:①②③④,
故答案为:①②③④.
点评 此题主要考查了圆的综合应用以及垂直平分线的性质、正方形的性质、全等三角形的判定及性质的而运用、圆的切线的判定方法的运用、勾股定理的性质的运用等知识,在解答中运用作辅助线制造全等三角形是关键.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
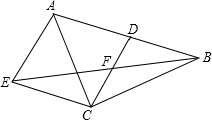 如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.
如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天我市下雨 | |
| B. | 抛一枚硬币,正面朝下 | |
| C. | 购买一张福利彩票中奖了 | |
| D. | 掷一枚骰子,向上一面的数字一定大于零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④.
如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com