
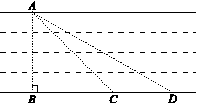
如图,为了估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BD,∠ACB=45°,∠ADB=30°,并且点B,C,D在同一条直线上.若测得CD=30米,求河宽AB(结果精确到1米,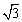 取1.73,
取1.73,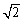 取1.41).
取1.41).
科目:初中数学 来源: 题型:
.阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做 四边形ABCD的边AB上的强相似点.解决问题:
四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写 出
出 的值.
的值.


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,过点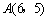 作AB⊥x轴于点B.半径为
作AB⊥x轴于点B.半径为 的⊙A
的⊙A
与AB交于点C,过B点作⊙A的切线BD,切点为D,连接DC并延长交x轴于点E.
(1)当 时,EB的长等于 ;
时,EB的长等于 ;
(2)点E的坐标为 (用含r的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.
问题:⊙O的半径为1,画一个⊙O的关联图形.

 |
 个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的 (它是非封闭的图形),它们都是⊙O的
个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的 (它是非封闭的图形),它们都是⊙O的 关联图形.而图2中以P,Q为端点的
关联图形.而图2中以P,Q为端点的 一条曲线就不是⊙O的关联图形.
一条曲线就不是⊙O的关联图形. 参考小明的发现,解决问题:
(1)在下列几何图形中,⊙O的关联图形是 (填序号);
① ⊙O的外切正多边形
② ⊙O的内接正多边形
③ ⊙O的一个半径大于1的同心圆
 (2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____;
(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____;
(3)在图2中,当⊙O的关联图形 的弧长最小时,经过D,E两点的直线为y =__;
(4 )请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
一枚质地均匀的正方体骰子,其六个面分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字不小于3的概率是( )
A.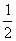 B.
B. 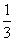 C.
C.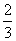 D.
D.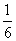
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在标有刻度的直线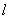 上,从点A开始,
上,从点A开始,
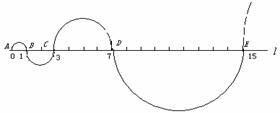 以AB=1为直径画半圆,记为第1个半圆;
以AB=1为直径画半圆,记为第1个半圆;
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆.
……,按此规律,连续画半圆,则第4个
半圆的面积是第3个半圆面积的 倍。第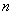 个半圆的面积为 .(结果保留
个半圆的面积为 .(结果保留 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com