
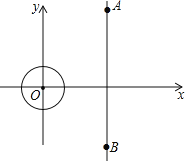
【题目】如图,在平面直角坐标系xOy中,![]() 的半径为1,A、B两点坐标分别为
的半径为1,A、B两点坐标分别为![]() 、
、![]() 已知点P是
已知点P是![]() 上的一点,点Q是线段AB上的一点,设
上的一点,点Q是线段AB上的一点,设![]() 的面积为S,当
的面积为S,当![]() 为直角三角形时,S的取值范围为______.
为直角三角形时,S的取值范围为______.
【答案】![]() ≤S≤
≤S≤![]() .
.
【解析】
根据△OPQ为直角三角形时,∠OQP不可能为90°,所以分两种情况:分别以O和P为直角顶点,根据直径所对的圆周角为直角,通过画辅助圆确定P和Q,画图,根据直角三角形面积公式计算可得结论.
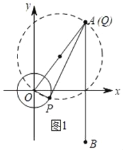
解:①当P为直角顶点时,
当OQ最长时,如图1,OQ=5,Q与A重合,PQ=![]() =2
=2![]() ,S大=
,S大=![]() ×1×2
×1×2![]() =
=![]() ,
,
当OQ最短时,OQ=3,此时OQ⊥AB,PQ=![]() =2
=2![]() ,S小=
,S小=![]() =
=![]() ;
;
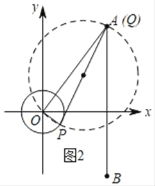
②当O为直角顶点时,如图2,
当Q与A重合时,OA最大,此时S=![]() ×1×5=
×1×5=![]() >
>![]() ,
,
当OQ⊥AB时,S最小,S=![]() =
=![]() ,
,
综上,当△OPQ为直角三角形时,S的取值范围为![]() ≤S≤
≤S≤![]() .
.
故答案为:![]() ≤ S ≤
≤ S ≤![]() .
.


科目:初中数学 来源: 题型:
【题目】已知矩形PMON的边OM、ON分别在x、y轴上,O为坐标原点,且点P的坐标为(﹣2,3).将矩形PMON沿x轴正方向平移4个单位,得到矩形P1M1O1N1再将矩形P1M1O1N1绕着点O1旋转90°得到矩形P2M2O2N2.在坐标系中画出矩形P2M2O2N2,并求出直线P1P2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(﹣2,﹣1),试确定平移的方向和平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
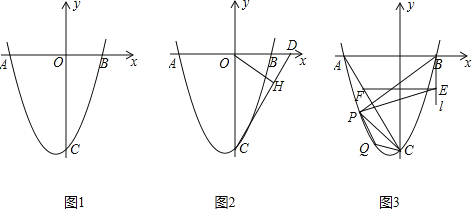
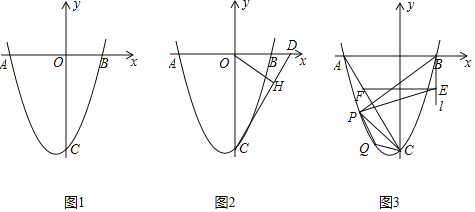
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
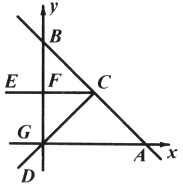
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 绕点
绕点![]() 按顺时针旋转,且
按顺时针旋转,且![]() ,
,![]() 的一边
的一边![]() 交
交![]() 轴于点
轴于点![]() ,开始时另一边
,开始时另一边![]() 经过点
经过点![]() ,点
,点![]() 坐标为
坐标为![]() ,当
,当![]() 旋转过程中,射线
旋转过程中,射线![]() 与
与![]() 轴的交点由点
轴的交点由点![]() 到点
到点![]() 的过程中,则经过点
的过程中,则经过点![]() 三点的圆的圆心所经过的路径长为( )
三点的圆的圆心所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com