
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)当![]() 时,
时,
①抛物线![]() 的对称轴为
的对称轴为![]() ________;
________;
②若在抛物线![]() 上有两点
上有两点![]() ,且
,且![]() ,则
,则![]() 的取值范围是________;
的取值范围是________;
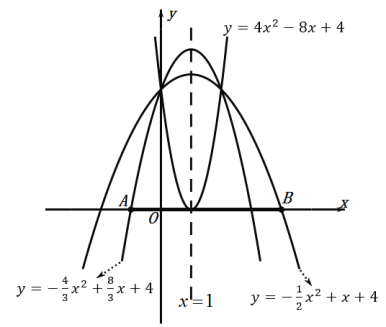
(2)抛物线![]() 的对称轴与
的对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,将点
轴对称,将点![]() 向右平移3个单位得到点
向右平移3个单位得到点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 恰有一个公共点,结合图象,求
恰有一个公共点,结合图象,求![]() 的取值范围.
的取值范围.
【答案】(1)①1;②![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①根据抛物线的对称轴公式即可求得;
②根据抛物线的对称性质,求得点![]() 的对称点为
的对称点为![]() ,根据函数图象即可求得答案;
,根据函数图象即可求得答案;
(2)根据平移的性质,分别求得A、B的坐标,依题意,根据函数图象,三种情况分类讨论,得出相应的a值,从而得结论.
(1)①抛物线![]() 的对称轴为:
的对称轴为:![]() ;
;
②∵抛物线![]() 关于
关于![]() 对称,
对称,
∴点![]() 的对称点为
的对称点为![]() ,
,
∵![]() ,
,
∴抛物线![]() 开口向上,
开口向上,
观察图象,![]() 或
或![]() 时,
时,![]() ;
;
故答案为:①1;②![]() 或
或![]() ;
;
(2)∵抛物线![]() 的对称轴为
的对称轴为![]() ,且对称轴与
,且对称轴与![]() 轴交于点
轴交于点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 右移3个单位得到点
右移3个单位得到点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
依题意,抛物线![]() 与线段
与线段![]() 恰有一个公共点,
恰有一个公共点,
把点![]() 代入
代入![]() 可得
可得![]() ;
;
把点![]() 代入
代入![]() 可得
可得![]() ;
;
把点![]() 代入
代入![]() 可得
可得![]() .
.
根据所画图象可知抛物线![]() 与线段
与线段![]() 恰有一个公共点时可得
恰有一个公共点时可得![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】近年来,移动支付已成为主要支付方式之一.为了解某校800名学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
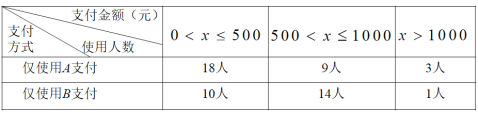
下面有四个推断:
①从全校学生中随机抽取1人,该学生上个月仅使用A支付的概率为0.3;
②从全校学生中随机抽取1人,该学生上个月A,B两种支付方式都使用的概率为0.45;
③估计全校仅使用B支付的学生人数为200人;
④这100名学生中,上个月仅使用A和仅使用B支付的学生支付金额的中位数为800元.
其中合理推断的序号是( )
A.①②B.①③C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
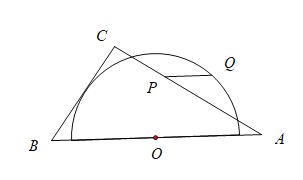
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心作半圆,使
为圆心作半圆,使![]() 与半圆相切,点
与半圆相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是( )
长的最大值与最小值的和是( )
A.8B.9C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具商店以每件60元为成本购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价1元,则每天可多卖2件.
(1)若商店打算每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为追求效益最大化,每件玩具的售价定为多少元时,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
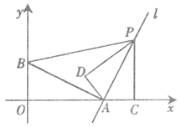
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
⑴方法感悟:
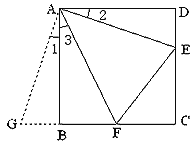
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
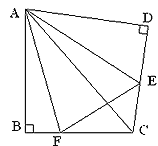
⑵方法迁移:
如图②,将![]() 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
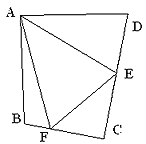
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足![]() ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com