
ЁОЬтФПЁПзлКЯгыЪЕМљЃК
ЮЪЬтЧщОГЃКдкОиаЮABCDжаЃЌЕуEЮЊBCБпЕФжаЕуЃЌНЋЁїABEбижБЯпAEЗелЃЌЪЙЕуBгыЕуFжиКЯЃЌжБЯпAFНЛжБЯпCDгкЕуG.
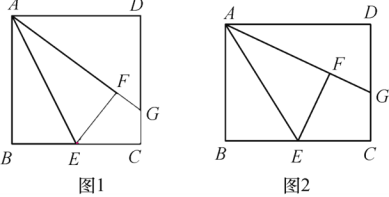
ЬиР§ЬНОПЁЁЪЕбщаЁзщЕФЭЌбЇЗЂЯжЃК
ЃЈ1ЃЉШчЭМ1ЃЌЕБABЃНBCЪБЃЌAGЃНBCЃЋCGЃЌЧыФужЄУїИУаЁзщЗЂЯжЕФНсТлЃЛ
ЃЈ2ЃЉЕБABЃНBCЃН4ЪБЃЌЧѓCGЕФГЄЃЛ
бгЩьЭиеЙЃКЃЈ3ЃЉЪЕжЊаЁзщЕФЭЌбЇдкЪЕбщаЁзщЕФЦєЗЂЯТЃЌНјвЛВНЬНОПСЫЕБABЁУBCЃН![]() ЁУ2ЪБЃЌЯпЖЮAGЃЌBCЃЌCGжЎМфЕФЪ§СПЙиЯЕЃЌЧыФужБНгаДГіЪЕжЊаЁзщЕФНсТлЃК___________ЃЎ
ЁУ2ЪБЃЌЯпЖЮAGЃЌBCЃЌCGжЎМфЕФЪ§СПЙиЯЕЃЌЧыФужБНгаДГіЪЕжЊаЁзщЕФНсТлЃК___________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉAGЃН![]() BCЃЋCG
BCЃЋCG
ЁОНтЮіЁП
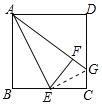
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгEGЃЎжЛвЊжЄУїЁїEGFЁеЁїEGCМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉжЛвЊжЄУїЁїABEЁзЁїECGЃЌМДПЩЭЦГі![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌСЌНгEGЃЎгЩЁїAEBЁеЁїAEFЃЌЁїEGFЁеЁїEGCЃЌЭЦГіAB=AFЃЌBE=EF=ECЃЌFG=GCЃЌгЩABЁУBC=BC=![]() ЁУ2ЃЌЭЦГіAB=
ЁУ2ЃЌЭЦГіAB=![]() BCЃЌПЩЕУAG=AF+FG=AB+CG=
BCЃЌПЩЕУAG=AF+FG=AB+CG=![]() BC+CGЃЎ
BC+CGЃЎ
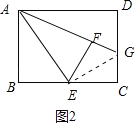
НтЃК(1)жЄУїЃКСЌНгEG.
ЁпЁїAEFЪЧгЩЁїAEBЗелЕУЕНЃЌЕуEЮЊBCБпЕФжаЕуЃЌ
ЁрEBЃНEFЃНECЃЌABЃНAFЃЌЁЯAFEЃНЁЯBЃНЁЯCЃН90Ёу.
дкRtЁїEGFКЭRtЁїEGCжаЃЌ![]() ЃЌ
ЃЌ
ЁрRtЁїEGFЁеRtЁїEGC(HL)ЃЎ
ЁрFGЃНGC.
ЁпABЃНAFЃНBCЃЌ
ЁрAGЃНAFЃЋFGЃНBCЃЋCG.
(2)ЁпЁїEGFЁеЁїEGCЃЌ
ЁрЁЯGEFЃНЁЯGEC.
ЁпЁЯAEBЃНЁЯAEFЃЌЁЯBECЃН180ЁуЃЌ
ЁрЁЯAEGЃН90Ёу.
ЁрЁЯAEBЃЋЁЯGECЃН90ЁуЃЌЁЯAEBЃЋЁЯBAEЃН90Ёу.
ЁрЁЯGECЃНЁЯBAE.
ЁпЁЯBЃНЁЯCЃЌ
ЁрЁїABEЁзЁїECG.
Ёр![]()
ЁпECЃН2ЃЌ
ЁрCGЃН1ЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌСЌНгEGЃЎ
ЁпЁїAEBЁеЁїAEFЃЌЁїEGFЁеЁїEGCЃЌ
ЁрAB=AFЃЌBE=EF=ECЃЌFG=GCЃЌ
ЁпABЃКBC=BC=![]() ЁУ2ЃЌ
ЁУ2ЃЌ
ЁрAB=![]() BCЃЌ
BCЃЌ
ЁрAG=AF+FG=AB+CG=![]() BC+CGЃЎ
BC+CGЃЎ
МДAG=![]() BC+CGЃЎ
BC+CGЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЕФЖЅЕуЪЧ
ЃЉЕФЖЅЕуЪЧ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгыжБЯп
ЃЌгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() .Й§Еу
.Й§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЦНвЦХзЮяЯп
ЃЌЦНвЦХзЮяЯп![]() ЪЙЦфОЙ§Еу
ЪЙЦфОЙ§Еу![]() ЁЂ
ЁЂ![]() ЕУЕНХзЮяЯп
ЕУЕНХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉЃЌХзЮяЯп
ЃЉЃЌХзЮяЯп![]() гы
гы![]() жсЕФСэвЛИіНЛЕуЮЊ
жсЕФСэвЛИіНЛЕуЮЊ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ
ЕФзјБъ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ3ЃЉШєЫФБпаЮ![]() ЮЊОиаЮЃЌ
ЮЊОиаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЮхБпаЮABCDEФкНггкЁбOЃЌЙ§ЕуAзїЁбOЕФЧаЯпНЛЖдНЧЯпDBЕФбгГЄЯпгкЕуFЃЌдђЯТСаНсТлВЛГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ

A. AEЁЮBD B. AB=BF C. AFЁЮCD D. DF=![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌDЁЂEЗжБ№ЪЧBCКЭCBбгГЄЯпЩЯЕФЕуЃЌЧв![]() ЃЌСЌНгADЁЂAEЃЌBMЁЂCNЗжБ№ЪЧЁїABEКЭЁїACDЕФИпЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌ BGЁЂCHЗжБ№ЪЧЁЯABEКЭЁЯACDЕФЦНЗжЯпЃЌЗжБ№НЛAEЁЂADгкЕуGЁЂH.
ЃЌСЌНгADЁЂAEЃЌBMЁЂCNЗжБ№ЪЧЁїABEКЭЁїACDЕФИпЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌ BGЁЂCHЗжБ№ЪЧЁЯABEКЭЁЯACDЕФЦНЗжЯпЃЌЗжБ№НЛAEЁЂADгкЕуGЁЂH.
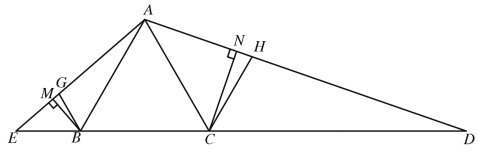
жЄУї:(1)ЁїABEЁзЁїDCA;
(2)sinЁЯMBG=sinЁЯNCH.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГБіЙнгаПЭЗП![]() МфЙЉгЮПЭОгзЁЃЌЕБУПМфПЭЗПЕФЖЈМлЮЊУПЬь
МфЙЉгЮПЭОгзЁЃЌЕБУПМфПЭЗПЕФЖЈМлЮЊУПЬь![]() дЊЪБЃЌПЭЗПЧЁКУШЋВПзЁТњЃЛШчЙћУПМфПЭЗПУПЬьЕФЖЈМлУПдіМг
дЊЪБЃЌПЭЗПЧЁКУШЋВПзЁТњЃЛШчЙћУПМфПЭЗПУПЬьЕФЖЈМлУПдіМг![]() дЊЃЌОЭЛсМѕЩй
дЊЃЌОЭЛсМѕЩй![]() МфПЭЗПГізтЃЎЩшУПМфПЭЗПУПЬьЕФЖЈМлдіМг
МфПЭЗПГізтЃЎЩшУПМфПЭЗПУПЬьЕФЖЈМлдіМг![]() дЊЃЌБіЙнГізтЕФПЭЗПЮЊ
дЊЃЌБіЙнГізтЕФПЭЗПЮЊ![]() МфЃЎЧѓЃК
МфЃЎЧѓЃК
![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ШчЙћФГЬьБіЙнПЭЗПЪеШы
ШчЙћФГЬьБіЙнПЭЗПЪеШы![]() дЊЃЌФЧУДетЬьУПМфПЭЗПЕФМлИёЪЧЖрЩйдЊЃП
дЊЃЌФЧУДетЬьУПМфПЭЗПЕФМлИёЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
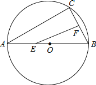
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвBC=4cmЃЌFЪЧЯвBCЕФжаЕуЃЌЁЯABC=60ЁуЃЎШєЖЏЕуEвд1cm/sЕФЫйЖШДгAЕуГіЗЂдкABЩЯбизХAЁњBдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊt(s)(0ЁмtЃМ8)ЃЌСЌНгEFЃЌЕБЁїBEFЪЧжБНЧШ§НЧаЮЪБЃЌt(s)ЕФжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮЕФБпOAдкxжсЩЯЃЌБпOCдкyжсЩЯЃЌЕуBЕФзјБъЮЊЃЈ10ЃЌ8ЃЉЃЌбижБЯпODелЕўОиаЮЃЌЪЙЕуAе§КУТфдкBCЩЯЕФEДІЃЌEЕузјБъЮЊЃЈ6ЃЌ8ЃЉЃЌХзЮяЯпy=ax2+bx+cОЙ§OЁЂAЁЂEШ§ЕуЃЎ
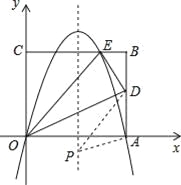

ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓADЕФГЄЃЛ
ЃЈ3ЃЉЕуPЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЖЏЕуЃЌЕБЁїPADЕФжмГЄзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
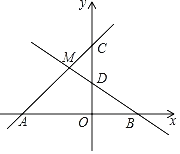
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНx+3ЗжБ№гыxжсЁЂyжсНЛгкЕуAЁЂCЃЌжБЯпyЃНmx+![]() ЗжБ№гыxжсЁЂyжсНЛгкЕуBЁЂDЃЌжБЯпACгыжБЯпBDЯрНЛгкЕуMЃЈЉ1ЃЌbЃЉ
ЗжБ№гыxжсЁЂyжсНЛгкЕуBЁЂDЃЌжБЯпACгыжБЯпBDЯрНЛгкЕуMЃЈЉ1ЃЌbЃЉ
ЃЈ1ЃЉВЛЕШЪНx+3Ёмmx+![]() ЕФНтМЏЮЊЁЁ ЁЁЃЎ
ЕФНтМЏЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧѓжБЯпACЁЂжБЯпBDгыxжсЫљЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
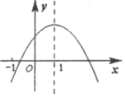
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃКЂй
ЕФЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЎЦфжае§ШЗЕФЪЧ________________ЃЎ
ЃЎЦфжае§ШЗЕФЪЧ________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com