
����Ŀ����ͼ����ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC����DAE��90�㣬��PΪֱ��BD��CE�Ľ��㣮
��1����ͼ������ADE�Ƶ�A��ת����D���߶�CE��ʱ������BE�����и����������ۣ���BD��CD+![]() AD����BE2��2��AD2+AB2����������ȷ������ ����������֤����
AD����BE2��2��AD2+AB2����������ȷ������ ����������֤����
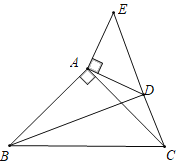
��2����AB��4��AD��2���ѡ�ADE�Ƶ�A��ת��
������EAC��90��ʱ����PB�ij���
����ת�������߶�PB�������ֵ���� ����
���𰸡���1������֤�������������2����PB��![]() ����2
����2![]() +2��
+2��
��������
��1����������֤����ABD�ա�ACE���Ϳ��Եõ����ۣ�����BDEΪֱ�������ξͿ��Եó�BE2��BD2+DE2������DAE����BAC�ǵ���ֱ�������ξ���DE2��2AD2��BC2��2AB2������BC2��BD2+CD2��BD2�Ϳ��Եó����ۣ�
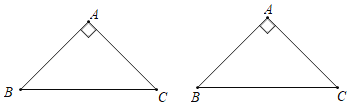
��2�����������ε���E��AB��ʱ��BE��AB��AE��2������PEB�ס�AEC����![]() ���ɴ˼��ɽ�����⣻����E��BA�ӳ�����ʱ��BE��6���ⷨ���ƣ�
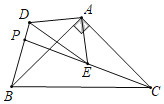
���ɴ˼��ɽ�����⣻����E��BA�ӳ�����ʱ��BE��6���ⷨ���ƣ�
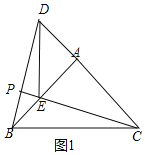
����ͼ3�У���AΪԲ��ADΪ�뾶��Բ����CE�ڡ�A�Ϸ����A����ʱ��PB��ֵ��ֱ����PB���ɣ�
��1���ߡ�ABC����ADE���й�������ĵ���ֱ�������Σ�
��AE��AD��AB��AC����DAE����BAC��90����DE��![]() AD��
AD��
���DAB����EAC����AE��AD��AB��AC��
���AEC�ա�ADB��SAS��
��BD��CE��DE+CD��
��BD��CD+![]() AD��
AD��
�����ȷ��
��BD��CE��
��BE2��BD2+DE2��
�ߡ�BAC����DAE��90����AB��AC��AD��AE��
��DE2��2AD2��BC2��2AB2��
��BC2��BD2+CD2��BD2��
��2AB2��BD2+CD2��BD2��
��BE2��2��AD2+AB2����
��ڴ���
�ʴ�Ϊ�٣�
��2����ͼ1�У�����E��AB��ʱ��BE��AB��AE��2��
�ߡ�EAC��90����
��CE��![]() ��
��![]() ��2
��2![]() ��
��
ͬ��1����֤��ADB�ա�AEC��
���DBA����ECA��
�ߡ�PEB����AEC��
���PEB�ס�AEC��
��![]() ��
��
��![]()
��PB��![]() ��
��
��ͼ2�У�����E��BA�ӳ�����ʱ��BE��AB+AE��6��

�ߡ�EAC��90����
��CE��![]() ��
��![]() ��2
��2![]() ��
��
ͬ��1����֤��ADB�ա�AEC��
���DBA����ECA��
�ߡ�BEP����CEA��
���PEB�ס�AEC��
��![]() ��
��
��![]() ��
��
��PB��![]() ��
��
���ϣ�PB��![]() ��
��![]() ��
��
����ͼ3�У���AΪԲ��ADΪ�뾶��Բ����CE�ڡ�A�Ϸ����A����ʱ��PB��ֵ���
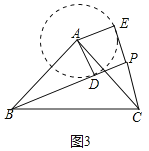
���ɣ���ʱ��BCE������PB�����PBC��ֱ�������Σ�б��BCΪ��ֵ����BCE������PB���
��AE��EC��
��EC��![]() ��
��![]() ��2
��2![]() ��
��
�ɣ�1����֪����ABD�ա�ACE��
���ADB����AEC��90����BD��CE��2![]() ��
��
���ADP����DAE����AEP��90����
���ı���AEPD�Ǿ��Σ�
��PD��AE��2��
��PB��BD+PD��2![]() +2��
+2��
����������PB�������ֵ��2![]() +2��
+2��
�ʴ�Ϊ��2![]() +2��
+2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �������
�������![]() ���ס������˴����س���������У����ȳ���.ͼ��
���ס������˴����س���������У����ȳ���.ͼ��![]() ��ʾ������
��ʾ������![]() �صľ���
�صľ���![]() ��ʱ��
��ʱ��![]() �Ĺ�ϵ�����ͼ�����н��۴�����ǣ� ��
�Ĺ�ϵ�����ͼ�����н��۴�����ǣ� ��
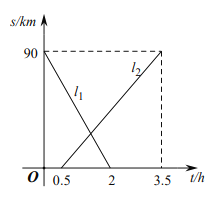
A.![]() �DZ�ʾ����
�DZ�ʾ����![]() �صľ�����ʱ���ϵ��ͼ��
�صľ�����ʱ���ϵ��ͼ��
B.�ҵ��ٶ���![]()
C.��������ʱ����![]()
D.�������յ�ʱ�Ҿ����յ㻹��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
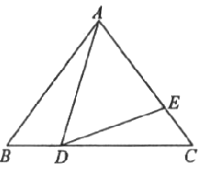
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() ��
��![]() ���ϵĶ��㣨����
���ϵĶ��㣨����![]() �غϣ�����
�غϣ�����![]() ��
��![]() ���ϣ���������
���ϣ���������![]() .
.
��1����֤��![]() ��
��
��2����![]() �ij�Ϊ
�ij�Ϊ![]() �����ú�
�����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��3������2���е�![]() ���ʱ����
���ʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���߶�![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
Ϊ����![]() ��һ�㣬
��һ�㣬![]() ƽ��
ƽ��![]() ���߶�
���߶�![]() �ڵ�
�ڵ�![]() ������˵�
������˵�![]() ��
��![]() �غϣ�.
�غϣ�.

��1����![]() Ϊ��ǣ���
Ϊ��ǣ���![]() ʱ�����ı���
ʱ�����ı���![]() �������
�������
��2����![]() ��
��![]() ����ʱ�����߶�
����ʱ�����߶�![]() �ij���
�ij���
��3����![]() ��
��![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ����д��������.
�ĺ�����ϵʽ����д��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У���D�� AB����һ�㣬����CD�����߶�CD�Ƶ�C��˳ʱ�뷽����ת60����õ�CE������AE����֤��AE��BC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ������
����ͼ������![]() ��
��![]() �ֱ�Ϊ����
�ֱ�Ϊ����![]() �ϵĶ��㣨��C��E�������B�غϣ�������AC��AEʹ��
�ϵĶ��㣨��C��E�������B�غϣ�������AC��AEʹ��![]() ������
������![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() .
.
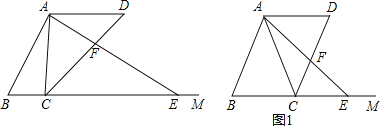
��1����ͼ1����![]() ʱ����AF�ij�.
ʱ����AF�ij�.
��2������![]() �ڵ�
�ڵ�![]() ���Ҳ�ʱ����
���Ҳ�ʱ����![]() ����
����![]() �ĺ�����ϵʽ����д�������Ķ�����.
�ĺ�����ϵʽ����д�������Ķ�����.
��3������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ǵ��������Σ�ֱ��д��
�ǵ��������Σ�ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
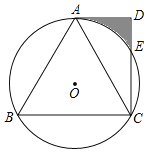
����Ŀ����ͼ����OΪ�ȱߡ�ABC�����Բ��AD��BC����ADC��90����CD����O�ڵ�E��
��1����֤��AD�ǡ�O�����ߣ�
��2����DE��2������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�ؽ�������ƶ�����Ծ���ƶ������ʵ������ȣ��ִ�ȫ�ؽ�������ƶ�����������ȡ�˲���ƶ���������˵��飨�ѵ�������Ϊ�ĸ��ȼ���A�����dz����⣺B�����⣻C�����������⣺D���������⣩���������������Ƴ���������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺
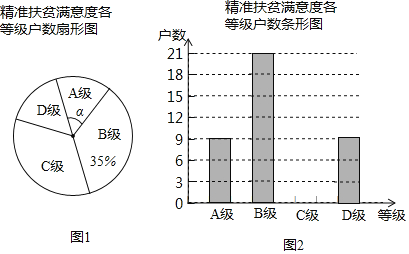
��1�����γ���������ԵĽ�������ƶ�������ܻ������� ����
��2��ͼ���У������Ķ������� ��������ͼ������ͳ��ͼ����������
��3��ij�ؽ�������ƶ������10000�������ȫ���μ��������ȵ��飬����Ʒdz�����Ļ���ԼΪ���ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ΪԲ������
ΪԲ������![]() ����
����![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��
Ϊ��![]() �ϲ�ͬ��
�ϲ�ͬ��![]() ��
��![]() ������һ�㣬����
������һ�㣬����![]() ��
��![]() ����
����![]() ��ֱ���
��ֱ���![]() ��
��![]() ��
��![]() ��
��![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() ����
����![]() ���ڡ�
���ڡ�![]() ��˳ʱ��ӵ�
��˳ʱ��ӵ�![]() �˶�����
�˶�����![]() �Ĺ����У�����ͼ�����ܱ�ʾ
�Ĺ����У�����ͼ�����ܱ�ʾ![]() ��
��![]() �ĺ�����ϵ�IJ���ͼ���ǣ� ��
�ĺ�����ϵ�IJ���ͼ���ǣ� ��

A.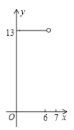 B.
B.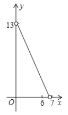 C.
C.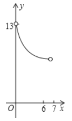 D.
D.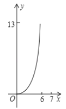
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com