
【题目】在平面直角坐标系中,已知![]() ,函数
,函数![]() 的图象与
的图象与![]() 轴有
轴有![]() 个交点,函数
个交点,函数![]() 的图象与
的图象与![]() 轴有
轴有![]() 个交点,则
个交点,则![]() 与
与![]() 的数量关系是( )
的数量关系是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】C
【解析】
先把两个函数化为一般形式,若为二次函数,计算根的判别式可确定图象与x轴的交点个数,若为一次函数,则与x轴只有一个交点,据此即可得答案.
∵![]() =x2+(a+b)x+ab,
=x2+(a+b)x+ab,
∴△=(a+b)2-4ab=(a-b)2,
∵a≠b,
∴△=(a-b)2>0,
∴函数![]() 的图象与x轴用2个交点,
的图象与x轴用2个交点,
∴m=2.
∵函数![]() =abx2+(a+b)x+1,
=abx2+(a+b)x+1,
∴当ab≠0时,函数![]() 是二次函数,
是二次函数,
∴△=(a+b)2-4ab=(a-b)2,
∵a≠b,
∴△=(a-b)2>0,
∴函数![]() 的图象与x轴有2个交点,
的图象与x轴有2个交点,
∴n=2,
∴m=n,
当ab=0时,
∵a≠b,
∴函数为y=ax+1或y=ax+1,都是一次函数,
∴函数与x轴只有1个交点,
∴n=1,
∴m=n+1,
∴m与n的数量关系是m=n,或m=n+1,
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于![]() ,超过
,超过![]() 时,所有这种水果的批发单价均为3元
时,所有这种水果的批发单价均为3元![]() .图中折线表示批发单价
.图中折线表示批发单价![]() (元
(元![]() )与质量
)与质量![]() 的函数关系.
的函数关系.
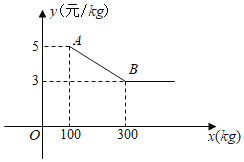
(1)求图中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润![]() 最大,最大利润是多少元?
最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(按要求方法解方程,否则不得分,没有要求的请用适当的方法解方程)
(1)![]() (直接开方法) (2)
(直接开方法) (2)![]() (配方法)
(配方法)
(3)![]() (公式法) (4)
(公式法) (4)![]() (因式分解法)
(因式分解法)
(5)![]() (6)
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() 垂直
垂直![]() .
.
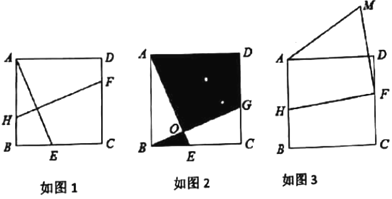
(1)如图1,求证:![]() ;
;
(2)如图2,平移线段![]() 至线段
至线段![]() ,
,![]() 交
交![]() 于点
于点![]() ,图中阴影部分的面积与正方形的面积之比为
,图中阴影部分的面积与正方形的面积之比为![]() ,求
,求![]() 的周长;
的周长;
(3)如图3,若![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至线段
至线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于半径为
中,对于半径为![]() 的
的![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称
,则称![]() 为
为![]() 的“近外点”.
的“近外点”.
(1)当![]() 的半径为2时,点
的半径为2时,点![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]() 的“近外点”是__________;
的“近外点”是__________;
(2)若点![]() 是
是![]() 的“近外点”,求
的“近外点”,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)当![]() 的半径为2时,直线
的半径为2时,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的“近外点”,直接写出
的“近外点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作矩形”的尺规作图过程,已知:![]()
求作:矩形![]()
作法:如图,
①作线段![]() 的垂直平分线角交
的垂直平分线角交![]() 于点
于点![]() ;
;
②连接![]() 并延长,在延长线上截取
并延长,在延长线上截取![]()
③连接![]()
所以四边形![]() 即为所求作的矩形
即为所求作的矩形
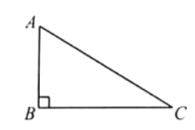
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:![]() ,
,![]() ,
,
![]() 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)
![]()
![]() 四边形
四边形![]() 是矩形( )(填推理的依据)
是矩形( )(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com