
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
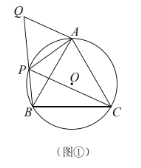
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
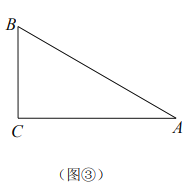
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;

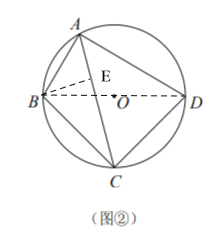
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先根据同弧所对的圆周角相等证明三角形ABC为等边三角形,得到∠ACB=60°,再求出∠APB=60°,根据AQ=AP判定△APQ为等边三角形,∠AQP=∠QAP=60°,故∠ACB=∠AQP,可判断∠QAC>120°,∠QBC<120°,故∠QAC≠∠QBC,可证四边形![]() 是准平行四边形;
是准平行四边形;
(2)根据已知条件可判断∠ABC≠∠ADC,则可得∠BAD=∠BCD=90°,连接BD,则BD为直径为10,根据BC=CD得△BCD为等腰直角三角形,则∠BAC=∠BDC=45°,在直角三角形BCD中利用勾股定理或三角函数求出BC的长,过B点作BE⊥AC,分别在直角三角形ABE和△BEC中,利用三角函数和勾股定理求出AE、CE的长,即可求出AC的长.
(3)根据已知条件可得:∠ADC=∠ABC=60°,延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),连接BO交弧AE于D点,则此时BD的长度最大,根据已知条件求出BO、OD的长度,即可求解.
(1)∵![]()
∴∠ABC=∠BAC=60°
∴△ABC为等边三角形,∠ACB=60°
∵∠APQ=180°-∠APC-∠CPB=60°
又AP=AQ
∴△APQ为等边三角形
∴∠AQP=∠QAP=60°
∴∠ACB=∠AQP
∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB>120°
故∠QBC=360°-∠AQP-∠ACB-∠QAC<120°
∴∠QAC≠∠QBC
∴四边形![]() 是准平行四边形
是准平行四边形
(2)连接BD,过B点作BE⊥AC于E点
∵准平行四边形![]() 内接于
内接于![]() ,
,![]()
∴∠ABC≠∠ADC,∠BAD=∠BCD
∵∠BAD+∠BCD=180°
∴∠BAD=∠BCD=90°
∴BD为![]() 的直径
的直径
∵![]() 的半径为5
的半径为5
∴BD=10
∵BC=CD,∠BCD=90°
∴∠CBD=∠BDC=45°
∴BC=BD![]() sin∠BDC=10
sin∠BDC=10![]() ,∠BAC=∠BDC=45°
,∠BAC=∠BDC=45°
∵BE⊥AC
∴∠BEA=∠BEC=90°
∴AE=AB![]() sin∠BAC=6
sin∠BAC=6![]()
![]()
∵∠ABE=∠BAE=45°
∴BE=AE=![]()
在直角三角形BEC中,EC=![]()
∴AC=AE+EC=![]()
(3)在![]() 中,
中,![]()
∴∠ABC=60°
∵四边形![]() 是准平行四边形,且
是准平行四边形,且![]()
∴∠ADC=∠ABC=60°
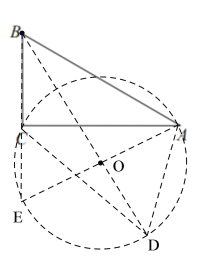
延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,因为∠ACE=90°,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),此时,∠ADC=∠AEC=60°,连接BO交弧AE于D点,则此时BD的长度最大.
在等边三角形ABE中,∠ACB=90°,BC=2
∴AE=BE=2BC=4
∴OE=OA=OD=2
∴BO⊥AE
∴BO=BE![]() sin∠E=4
sin∠E=4![]()
∴BD=BO+0D=2+![]()
即BD长的最大值为2+![]()


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
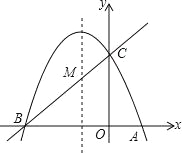
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 为常数,
为常数,![]() )的图象经过
)的图象经过![]() 两点.
两点.
(1)求该反比例函数的解析式和![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)若![]() 为直线
为直线![]() 上的一个动点,当
上的一个动点,当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
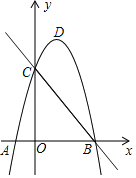
【题目】如图,已知直线y1=﹣x+3与x轴交于点B,与y轴交于点C,抛物y2=ax2+bx+c经过点B,C并与x轴交于点A(﹣1,0).
(1)求抛物线解析式,并求出抛物线的顶点D坐标 ;
(2)当y2<0时、请直接写出x的取值范围 ;
(3)当y1<y2时、请直接写出x的取值范围 ;
(4)将抛物线y2向下平移,使得顶点D落到直线BC上,求平移后的抛物线解析式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.
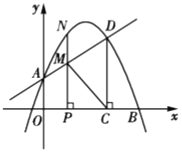
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
②设![]() 的长为
的长为![]() ,是否存在
,是否存在![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
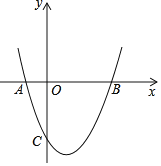
【题目】已知:抛物线y=x2﹣2(m﹣1)x﹣1﹣m
(1)当m=2时,求该抛物线的对称轴和顶点坐标;
(2)设该抛物线与x轴交于A(x1,0)、B(x2,0),x1<0<x2,与y轴交于点C,且满足![]() ,求这个抛物线的解析式;
,求这个抛物线的解析式;
(3)在(2)的条件下,是否存在着直线y=kx+b与抛物线交于点P、Q,使y轴平分△CPQ的面积?若存在,求出k,b应满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,点E, F分别在BC, BD上,且BE=1,过三点C, E, F作⊙O交CD于点G.
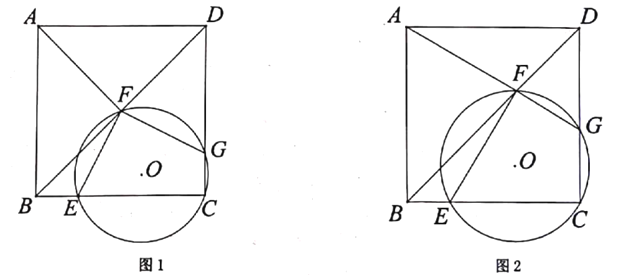
(1)证明∠EFG =90°.
(2)如图2,连结AF,当点F运动至点A,F, G三点共线时,求![]() 的面积.
的面积.
(3)在点F整个运动过程中,
①当EF, FG, CG中满足某两条线段相等,求所有满足条件的BF的长.
②连接EG,若![]() 时,求⊙O的半径(请直接写出答案) .
时,求⊙O的半径(请直接写出答案) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)小球飞行时间是多少时,小球最高?最大高度是多少?
(2)小球飞行时间t在什么范围时,飞行高度不低于15m?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com