
 有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米.
有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是$\frac{\sqrt{2}}{4}$米. 分析 连接扇形的两个端点,则是直径,因而扇形的半径是2•sin45°=$\sqrt{2}$,扇形的弧长l=$\frac{90π•\sqrt{2}}{180}=\frac{\sqrt{2}π}{2}$,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
解答 解:设底面圆的半径为r,则$\frac{\sqrt{2}π}{2}$=2πr,
∴r=$\frac{\sqrt{2}}{4}$m
圆锥的底面圆的半径长为$\frac{\sqrt{2}}{4}$米,
故答案为:$\frac{\sqrt{2}}{4}$米
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
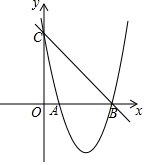 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
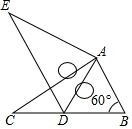 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )| A. | 0.5 | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com