
我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,则称这条直线与这个正方形相交.已知:如图,在平面直角坐标系中,正方形OABC的顶点坐标分别为 O(0,0),A(1,0),B(1,1),C(0,1).
(1)判断直线y=![]() x+
x+![]() 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;
(2)设d是点O到直线y=-![]() x+b的距离,若直线y=-
x+b的距离,若直线y=-![]() x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.
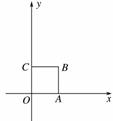
解:(1)相交. (2分)
∵直线y=![]() x+
x+![]() 与线段OC交于点(0,
与线段OC交于点(0,![]() ) 同时 (3分)
) 同时 (3分)
直线y=![]() x+
x+![]() 与线段CB交于点(
与线段CB交于点(![]() ,1), (4分)
,1), (4分)
∴直线y=![]() x+
x+![]() 与正方形OABC相交.
与正方形OABC相交.
(2)当直线y=-![]() x+b经过点B时,
x+b经过点B时,
即有1=-![]() +b,
+b,
∴b=![]() +1.
+1.
即 y=-![]() x+1+
x+1+![]() . (5分)
. (5分)
记直线y=-![]() x+1+
x+1+![]() 与x,y轴的交点分别为D,E.
与x,y轴的交点分别为D,E.
则D(![]() ,0),E(0,1+
,0),E(0,1+![]() ). (6分)
). (6分)
法1:在Rt△BAD中,tan∠BDA=![]() =
=![]() =
=![]() ,
,
∴∠EDO=60°, ∠OED=30°.
过O作OF1⊥DE,垂足为F1,则OF1=d1. (7分)
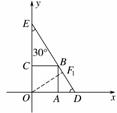
在Rt△OF1E中,∵∠OED=30°,
∴d1=![]() . (8分)
. (8分)
法2:∴DE=![]() (3+
(3+![]() ).
).
过O作OF1⊥DE,垂足为F1,则OF1=d1. (7分)
∴d1=![]() ×(1+
×(1+![]() )÷[
)÷[![]() (3+
(3+![]() )]
)]
=![]() . (8分)
. (8分)
∵直线y=-![]() x+b与直线y=-
x+b与直线y=-![]() x+1+
x+1+![]() 平行.
平行.
法1:当直线y=-![]() x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O,B重合.故直线y=-
x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O,B重合.故直线y=-![]()
x+b也一定与线段OF1相交,记交点为F,则F不与点O,F1重合,且OF=d. (9分)
∴当直线y=-![]() x+b与正方形相交时,
x+b与正方形相交时,
有0<d<![]() . (10分)
. (10分)
法2:当直线y=-![]() x+b与直线y=x(x>0)相交时,
x+b与直线y=x(x>0)相交时,
有 x=-![]() x+b,即x=
x+b,即x=![]() .
.
①当0<b<1+![]() 时,0<x<1,0<y<1.
时,0<x<1,0<y<1.
此时直线y=-![]() x+b与线段OB相交,且交点不与点O,B重合.
x+b与线段OB相交,且交点不与点O,B重合.
②当b>1+![]() 时,x>1,
时,x>1,
此时直线y=-![]() x+b与线段OB不相交.
x+b与线段OB不相交.
而当b≤0时,直线y=-![]() x+b不经过第一象限,即与正方形OABC不相交.
x+b不经过第一象限,即与正方形OABC不相交.
∴当0<b<1+![]() 时,直线y=-
时,直线y=-![]() x+b与正方形OABC相交. (9分)
x+b与正方形OABC相交. (9分)
此时有0<d<![]() . (10分)
. (10分)


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
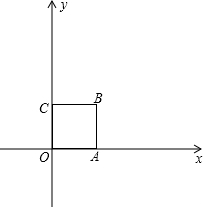 我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.
我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.| 1 |
| 3 |
| 5 |
| 6 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年3月中考数学模拟试卷(21)(解析版) 题型:解答题
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;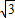 x+b的距离,若直线y=-
x+b的距离,若直线y=-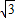 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.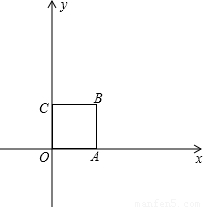
查看答案和解析>>
科目:初中数学 来源:2011年江苏省扬州中学树人学校中考数学一模试卷(解析版) 题型:解答题
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;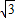 x+b的距离,若直线y=-
x+b的距离,若直线y=-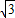 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.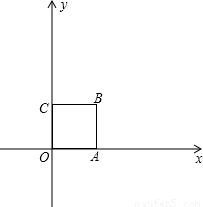
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;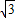 x+b的距离,若直线y=-
x+b的距离,若直线y=-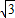 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.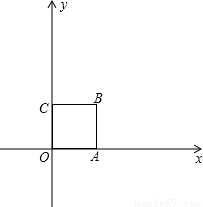
查看答案和解析>>
科目:初中数学 来源:2009年福建省厦门市中考数学试卷(解析版) 题型:解答题
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由; x+b的距离,若直线y=-
x+b的距离,若直线y=-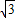 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com