
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 与
与![]() 关于
关于![]() 轴对称,交
轴对称,交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 在
在![]() 外作直线
外作直线![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 于点
于点 ![]() .求证:
.求证:![]()
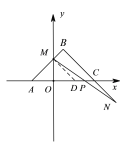
(3)如图2,如果![]() 沿
沿![]() 轴向右平移,
轴向右平移,![]() 边交
边交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 的延长线上的一点,且
的延长线上的一点,且![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,在
,在![]() 平移的过程中,
平移的过程中,![]() 的长度是否为定值,请说明理由.
的长度是否为定值,请说明理由.

【答案】(1)![]() ;(2)见解析;(3)是,理由见解析
;(2)见解析;(3)是,理由见解析
【解析】
(1)先根据对称点的特点得出C点的坐标,然后利用待定系数法即可求出直线BC的解析式;
(2)首先通过等腰直角三角形的性质得出![]() ,然后证明
,然后证明![]() ,则有
,则有![]() ,最后利用
,最后利用![]() 即可证明;
即可证明;
(3)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,首先根据平行线的性质和等腰三角形的性质得出
,首先根据平行线的性质和等腰三角形的性质得出![]() ,进而可证
,进而可证![]() ,则有
,则有![]() ,最后利用
,最后利用![]() 则可证明OP为定值.
则可证明OP为定值.
解:(1)![]() ,直线
,直线![]() 与
与![]() 关于
关于![]() 轴对称,交
轴对称,交![]() 轴于点
轴于点![]() ,
,
∴点![]() 坐标是
坐标是![]() .
.
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 代入得:
代入得:
![]() 解得:
解得:![]()
∴直线BC的解析式为![]() ;
;
(2)![]() ,
,
![]() ,
,![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 中
中
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 为定值,理由如下:
为定值,理由如下:
过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为定值.
为定值.


科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于E.
(1)求∠AEC的度数;
(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售同型号A、B两种品牌节能灯管,它们进价相同,A品牌售价可变,最低售价不能低于进价,最高利润不超过4元,B品牌售价不变.它们的每只销售利润与每周销售量如下表:(售价=进价+利润)

(1)当A品牌每周销售量为300只时,B品牌每周销售多少只?
(2)A品牌节能灯管每只利润定为多少元时?可获得最大总利润,并求最大总利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的边
的边![]() 轴,垂足为点
轴,垂足为点![]() ,顶点
,顶点![]() 在第二象限,顶点
在第二象限,顶点![]() 在
在![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() ,
,![]() )的图像同时经过顶点
)的图像同时经过顶点![]() 、
、![]() ,若点
,若点![]() 的横坐标为1,
的横坐标为1,![]() .则
.则![]() 的值为( )
的值为( )

A.![]() B.3C.
B.3C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进入六月以来,西瓜出现热卖.佳佳水果超市用760元购进甲、乙两个品种的西瓜,销售完共获利360元,其进价和售价如表:
甲品种 | 乙品种 | |
进价(元/千克) | 1.6 | 1.4 |
售价(元/千克) | 2.4 | 2 |
(1)求佳佳水果超市购进甲、乙两个品种的西瓜各多少千克?
(2)由于销售较好,该超市决定,按进价再购进甲,乙两个品种西瓜,购进乙品种西瓜的重量不变,购进甲品种西瓜的重量是原来的2倍,甲品种西瓜按原价销售,乙品种西瓜让利销售.若两个品种的西瓜售完获利不少于560元,问乙品种西瓜最低售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段![]() 和折线
和折线![]() 表示“龟兔赛跑”时路程与时间的关系.请你根据图中给出的信息,解决下列问题.
表示“龟兔赛跑”时路程与时间的关系.请你根据图中给出的信息,解决下列问题.

(1)填空:折线![]() 表示赛跑过程中__________的路程与时间的关系,线段
表示赛跑过程中__________的路程与时间的关系,线段![]() 表示赛跑过程中__________的路程与时间的关系;
表示赛跑过程中__________的路程与时间的关系;
(2)兔子在起初每分钟跑多少千米?乌龟每分钟爬多少米?
(3)兔子醒来后,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子在途中一共睡了多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com