
 的速度向南偏东60°的BF方向移动,距沙尘暴中心200km的范围内是受沙
的速度向南偏东60°的BF方向移动,距沙尘暴中心200km的范围内是受沙 尘暴严重影响的区域.
尘暴严重影响的区域. AB=
AB= ×300=150<200,
×300=150<200,
 =
= =50
=50 ,
, ,
, =10,
=10, AB=
AB= ×300=150,即A市到沙尘暴移动路线的最短距离为150km,而距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域,由此判断A市必然会受到这次沙尘暴的影响;
×300=150,即A市到沙尘暴移动路线的最短距离为150km,而距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域,由此判断A市必然会受到这次沙尘暴的影响; =
= ,最后根据速度公式求出移动的时间即可.
,最后根据速度公式求出移动的时间即可.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
| 7 |
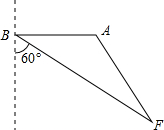 尘暴严重影响的区域.
尘暴严重影响的区域.查看答案和解析>>
科目:初中数学 来源:2009年山西省阳泉市郊区中考数学一模试卷(解析版) 题型:解答题
 的速度向南偏东60°的BF方向移动,距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域.
的速度向南偏东60°的BF方向移动,距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com