
如图,在等腰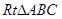 中,
中, ,
,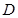 为斜边
为斜边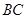 上的动点,若
上的动点,若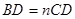 ,
,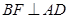 交
交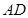 于
于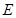 、
、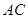 于
于 .
.
1.如图1,若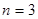 时,则
时,则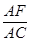 =
;
=
;
2.如图2,若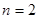 时,求证:
时,求证: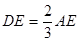
3.如图3,当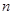 = 时,
= 时,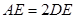 .
.
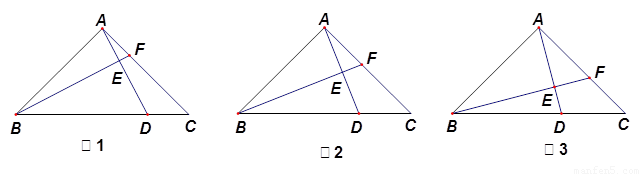
1.过C作CG⊥AC交AD的延长线与G点,如图1所示:
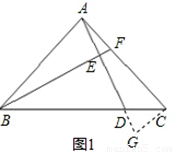
∵CG⊥AC,
∴CG∥AB.
∴△ABD∽△GCD.
∴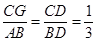 .
.
∵AB=AC,
∴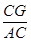 =
= .
.
∴tan∠EAF= .
.
∴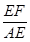 =
= .
.
∵在Rt△ABF中,△AEF∽△BAF,
∴ .
.
∴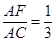 .
(3分)
.
(3分)
2.过D作DG∥BF交AC于G点,如图2所示:
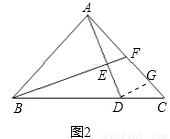
∵CD:DB=1:2,
∴CG:GF=1:2.
∵由第一问知AF:AC=CD:BD=1:2,
∴AF:FC=1:1.
∴AF:FG=3:2.
∴AE:ED=3:2.
∴DE=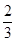 AE.
(8分)
AE.
(8分)
3.过D作DG∥BF交AC于G点,如图3所示:
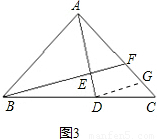
CD:BD=AF:AC=1:n,
CG:GF=1:n,
设CG=k,则:
GF=nk,
∵AE=2DE,
∴AF=2FG.
∴AF=2nk.
∴AC=3nk+k.
∵AC=nAF,
∴3nk+k=2n2k.
∴n=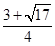 . (12分)
. (12分)
【解析】主要是考查辅助线的做法和相似三角形的判定和性质定理。


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com