
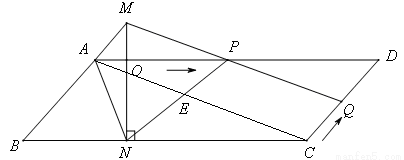
已知,如图,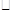 ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成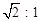 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
解:(1)若四边形AQDM是平行四边形,则PA=PD,反之也成立,
∵AD=3,PA=3t,∴PD=3-3t。
∴3t=3-3t,解得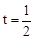 。
。
∴当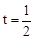 时,四边形AQDM是平行四边形。
时,四边形AQDM是平行四边形。
(2)∵四边形ABCD是平行四边形,∴AB∥CD。∴∠MAP=∠QDP。
又∵∠MPA=∠QPD,∴△MAP∽△QDP。
∴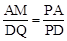 。∴
。∴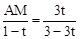 ,解得
,解得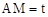 。
。
∵AB=CD=1,∴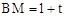 。
。
∵MN⊥BC,∠B=45°,∴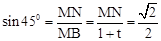 。∴
。∴ 。
。
又∵四边形ABCD是平行四边形,∴AD∥BC。
又∵MN⊥BC,∴MN⊥AD。
∴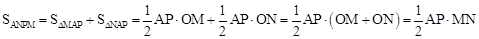
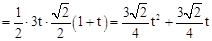 。
。
∴y与t之间的函数关系式为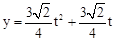 (0<t<1)。
(0<t<1)。
(3)存在。
假设存在某一时刻t,使四边形ANPM的面积是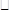 ABCD面积的一半, 则
ABCD面积的一半, 则
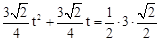 ,即
,即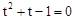 ,解得
,解得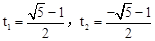 (舍去)。
(舍去)。
∴当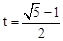 时,四边形ANPM的面积是
时,四边形ANPM的面积是 ABCD面积的一半。
ABCD面积的一半。
(4)存在。
假设存在某一时刻t,使NP与AC的交点把线段AC分成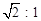 的两部分,
的两部分,
设NP与AC相交于点E,则AE:EC=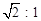 或AE:EC=
或AE:EC=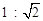 。
。
当AE:EC=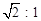 时,
时,
∵四边形ABCD是平行四边形,∴AD∥BC。∴△APE∽△CNE。
∴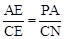 。∴
。∴ ,解得
,解得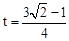 。
。
当AE:EC=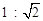 时,
时,
同理可得: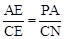 ,即
,即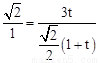 ,解得:
,解得: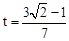 ,
,
∴当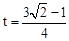 或
或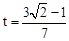 时,NP与AC的交点把线段AC分成
时,NP与AC的交点把线段AC分成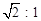 的两部分。
的两部分。
【解析】
试题分析:(1)根据若四边形AQDM是平行四边形,则PA=PD,列式即可得解。
(2)应用相似三角形和锐角三角函数的知识求出 ,从而应用转换思想,由
,从而应用转换思想,由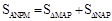
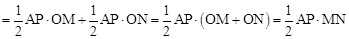 即可求得y与t之间的函数关系式。
即可求得y与t之间的函数关系式。
(3)假设存在某一时刻t,使四边形ANPM的面积是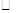 ABCD面积的一半, 则
ABCD面积的一半, 则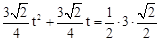 ,解出即可。
,解出即可。
(4)假设存在某一时刻t,使NP与AC的交点把线段AC分成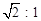 的两部分, 设NP与AC相交于点E,则分AE:EC=
的两部分, 设NP与AC相交于点E,则分AE:EC=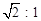 和AE:EC=
和AE:EC=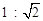 两种情况讨论即可。
两种情况讨论即可。


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 19、已知:如图,?ABCD中,对角线AC、BD交于点O.
19、已知:如图,?ABCD中,对角线AC、BD交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
 18、已知:如图梯形ABCD中,AD∥BC,AB=CD,AC与BD相交于点O.
18、已知:如图梯形ABCD中,AD∥BC,AB=CD,AC与BD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
 14、已知:如图,?ABCD.
14、已知:如图,?ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,?ABCD中,P为AB上任意一点,PQ∥AC交BC于Q.写出图中的两个三角形,同时满足条件:这两个三角形面积相等,且每个三角形的面积都小于?ABCD面积的一半.并证明你的结论.
已知:如图,?ABCD中,P为AB上任意一点,PQ∥AC交BC于Q.写出图中的两个三角形,同时满足条件:这两个三角形面积相等,且每个三角形的面积都小于?ABCD面积的一半.并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com