
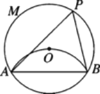
【题目】如图,在圆⊙O中,将弧AB沿弦AB折叠,使弧AB恰好经过圆心O,点P是优弧AMB上一点,则∠APB的度数为_________.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形” .下列判断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为![]() D. 事件M发生的概率为
D. 事件M发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:
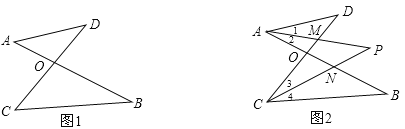
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:
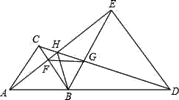
①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤FG∥AD.其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料;我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数0对应点之间的距离.这个结论可以推广为:
与数0对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.例:已知
对应点之间的距离.例:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与1的距离为2的点对应数为3和![]() ,即
,即![]() 的值为3和
的值为3和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,
,![]() 的值为__________;
的值为__________;
(2)若数轴上表示![]() 的点在
的点在![]() 与2之间,则
与2之间,则![]() 的值为__________;
的值为__________;
(3)当![]() 满足什么条件时,
满足什么条件时,![]() 有最小值,最小值是多少.
有最小值,最小值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() ,一只小虫从点
,一只小虫从点![]() 出发沿着数轴的正方向以每秒
出发沿着数轴的正方向以每秒![]() 个单位的速度爬行至
个单位的速度爬行至![]() 点,又立即返回到
点,又立即返回到![]() 点,共用了
点,共用了![]() 秒钟.
秒钟.
![]() 点
点![]() 对应的数是_.
对应的数是_.
![]() 若小虫返回到
若小虫返回到![]() 点后再作如下运动:第一次向右爬行
点后再作如下运动:第一次向右爬行![]() 个单位,第
个单位,第![]() 次向左爬行
次向左爬行![]() 个单位,第三次向右爬行
个单位,第三次向右爬行![]() 个单位,第四次向左爬行
个单位,第四次向左爬行![]() 个单位,..依此规律爬下去, 它第
个单位,..依此规律爬下去, 它第![]() 次爬行所停的点所对应的数是 .
次爬行所停的点所对应的数是 .
第![]() 次爬行所停的点所对应的数是
次爬行所停的点所对应的数是
![]() 在
在![]() 的条件下,求小虫第
的条件下,求小虫第![]() 次爬行所停的点所对应的数.
次爬行所停的点所对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com