
ЁОЬтФПЁПШчЭМЃЌЙЋЙВЦћГЕааЪЛдкБЪжБЕФЙЋТЗЩЯЃЌетЬѕТЗЩЯга![]() ЫФИіеОЕуЃЌУПЯрСкСНеОжЎМфЕФОрРыЮЊ
ЫФИіеОЕуЃЌУПЯрСкСНеОжЎМфЕФОрРыЮЊ![]() ЧЇУзЃЌДг
ЧЇУзЃЌДг![]() еОПЊЭљ
еОПЊЭљ![]() еОЕФГЕГЦЮЊЩЯааГЕЃЌДг
еОЕФГЕГЦЮЊЩЯааГЕЃЌДг![]() еОПЊЭљ
еОПЊЭљ![]() еОЕФГЕГЦЮЊЯТааГЕЃЎЕквЛАрЩЯааГЕЁЂЯТааГЕЗжБ№Дг
еОЕФГЕГЦЮЊЯТааГЕЃЎЕквЛАрЩЯааГЕЁЂЯТааГЕЗжБ№Дг![]() еОЁЂ
еОЁЂ![]() еОЭЌЪБЗЂГЕЃЌЯрЯђЖјааЃЌЧввдКѓЩЯааГЕЁЂЯТааГЕУПИє
еОЭЌЪБЗЂГЕЃЌЯрЯђЖјааЃЌЧввдКѓЩЯааГЕЁЂЯТааГЕУПИє![]() ЗжжгЗжБ№дк
ЗжжгЗжБ№дк![]() еОЭЌЪБЗЂвЛАрГЕЃЌГЫПЭжЛФмЕНеОЕуЩЯЁЂЯТГЕ(ЩЯЁЂЯТГЕЕФЪБМфКіТдВЛМЦ)ЃЌЩЯааГЕЁЂ ЯТааГЕЕФЫйЖШОљЮЊ
еОЭЌЪБЗЂвЛАрГЕЃЌГЫПЭжЛФмЕНеОЕуЩЯЁЂЯТГЕ(ЩЯЁЂЯТГЕЕФЪБМфКіТдВЛМЦ)ЃЌЩЯааГЕЁЂ ЯТааГЕЕФЫйЖШОљЮЊ![]() ЧЇУз/аЁЪБЃЎ
ЧЇУз/аЁЪБЃЎ
![]() ЕквЛАрЩЯааГЕЕН
ЕквЛАрЩЯааГЕЕН![]() еОЁЂЕквЛАрЯТааГЕЕН
еОЁЂЕквЛАрЯТааГЕЕН![]() еОЗжБ№гУЪБЖрЩйЃП
еОЗжБ№гУЪБЖрЩйЃП
![]() ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓЖрЩйаЁЪБЯрОр
ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓЖрЩйаЁЪБЯрОр![]() ЧЇУзЃП
ЧЇУзЃП
![]() вЛГЫПЭдк
вЛГЫПЭдк![]() СНеОжЎМфЕФ
СНеОжЎМфЕФ![]() ДІЃЌИеКУгіЕНЩЯааГЕЃЌ
ДІЃЌИеКУгіЕНЩЯааГЕЃЌ![]() ЧЇУзЃЌЫћДг
ЧЇУзЃЌЫћДг![]() ДІвд
ДІвд![]() ЧЇУз/аЁЪБЕФЫйЖШВНааЕН
ЧЇУз/аЁЪБЕФЫйЖШВНааЕН![]() еОГЫЯТааГЕЧАЭљ
еОГЫЯТааГЕЧАЭљ![]() еОАьЪТЃЎ
еОАьЪТЃЎ

ЂйШє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊМИЗжжгЃП
еОЕФЪБМфзюЩйвЊМИЗжжгЃП
ЂкШє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊМИЗжжгЃП
еОЕФЪБМфзюЩйвЊМИЗжжгЃП
ЁОД№АИЁПЃЈ1ЃЉЕквЛАрЩЯааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЌЕквЛАрЯТааГЕЕН
аЁЪБЃЌЕквЛАрЯТааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЛЃЈ2ЃЉЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ
аЁЪБЃЛЃЈ2ЃЉЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ![]() аЁЪБЛђ
аЁЪБЛђ![]() аЁЪБЯрОр
аЁЪБЯрОр![]() ЧЇУзЃЛЃЈ3ЃЉЂй
ЧЇУзЃЛЃЈ3ЃЉЂй![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЛЂк
ЗжжгЃЛЂк![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪБМф=ТЗГЬЁТЫйЖШМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр![]() ЧЇУзЃЌШЛКѓИљОнЯргіЧАКЭЯргіКѓЗжРрЬжТлЃЌЗжБ№СаГіЖдгІИіЗНГЬМДПЩЧѓГіtЃЛ
ЧЇУзЃЌШЛКѓИљОнЯргіЧАКЭЯргіКѓЗжРрЬжТлЃЌЗжБ№СаГіЖдгІИіЗНГЬМДПЩЧѓГіtЃЛ
ЃЈ3ЃЉгЩЬтвтжЊЃКЭЌЪБГіЗЂЕФвЛЖдЩЯЁЂЯТааГЕЕФЮЛжУЙигк![]() жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы
жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы![]() еОвВЪЧ
еОвВЪЧ![]() ЧЇУзЃЌетСОЯТааГЕРы
ЧЇУзЃЌетСОЯТааГЕРы![]() еОЪЧ
еОЪЧ![]() ЧЇУз
ЧЇУз
ЂйЯШЧѓГіЕуPЕНЕуBЕФЪБМфКЭГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг
еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФзюЩйЪБМфЃЛ
еОЕФзюЩйЪБМфЃЛ
ЂкЯШЧѓГіЕуPЕНЕуBЕФЪБМфКЭГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌШчВЛФмГЫЩЯЕквЛСОГЕЃЌЛЙашЫуГіФмЗёГЫЩЯгвВрЕкЖўСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг
еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌШчВЛФмГЫЩЯЕквЛСОГЕЃЌЛЙашЫуГіФмЗёГЫЩЯгвВрЕкЖўСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФзюЩйЪБМфЃЎ
еОЕФзюЩйЪБМфЃЎ
Нт:![]() ЕквЛАрЩЯааГЕЕН
ЕквЛАрЩЯааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЌ
аЁЪБЃЌ
ЕквЛАрЯТааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЛ
аЁЪБЃЛ
![]() ЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр
ЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр![]() ЧЇУзЃЎ
ЧЇУзЃЎ
ЂйЯргіЧА:
![]() ЃЎ
ЃЎ
НтЕУ![]()
ЂкЯргіКѓ:
![]()
НтЕУ![]()
Д№:ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ![]() аЁЪБЛђ
аЁЪБЛђ![]() аЁЪБЯрОр
аЁЪБЯрОр![]() ЧЇУзЃЛ
ЧЇУзЃЛ
(3)гЩЬтвтжЊЃКЭЌЪБГіЗЂЕФвЛЖдЩЯЁЂЯТааГЕЕФЮЛжУЙигк![]() жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы
жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы![]() еОвВЪЧ
еОвВЪЧ![]() ЧЇУзЃЌетСОЯТааГЕРы
ЧЇУзЃЌетСОЯТааГЕРы![]() еОЪЧ
еОЪЧ![]() ЧЇУзЃЎ
ЧЇУзЃЎ
ЂйШє![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ГЫПЭДг![]() ДІзпЕН
ДІзпЕН![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
ГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
![]()
![]() ГЫПЭФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЎ
ГЫПЭФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЎ
![]() (Зжжг)
(Зжжг)
Д№:Шє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ
ЂкШє![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ГЫПЭДг![]() ДІзпЕН
ДІзпЕН![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
ГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
![]()
![]() ГЫПЭВЛФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЌ
ГЫПЭВЛФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЌ
![]()
![]() ГЫПЭФмГЫЩЯгвВрЕкЖўСОЯТааГЕЃЎ
ГЫПЭФмГЫЩЯгвВрЕкЖўСОЯТааГЕЃЎ
![]() (Зжжг)
(Зжжг)
Д№:Шє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ


 аЁбЇЖсЙкABОэЯЕСаД№АИ
аЁбЇЖсЙкABОэЯЕСаД№АИ ABCПМЭѕШЋгХОэЯЕСаД№АИ
ABCПМЭѕШЋгХОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧвдBCЮЊЕзЕФЕШбќШ§НЧаЮЃЌADЪЧБпBCЩЯЕФИпЃЌЕуEЁЂFЗжБ№ЪЧABЁЂACЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAEDFЪЧСтаЮЃЛ
ЃЈ2ЃЉШчЙћЫФБпаЮAEDFЕФжмГЄЮЊ12ЃЌСНЬѕЖдНЧЯпЕФКЭЕШгк7ЃЌЧѓЫФБпаЮAEDFЕФУцЛ§SЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжНЁЩэЧђЃЌвбжЊетжжНЁЩэЧђЕФГЩБОМлЮЊУПИі20дЊЃЌЪаГЁЕїВщЗЂЯжЃЌИУжжНЁЩэЧђУПЬьЕФЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉгаШчЯТЙиЯЕЃКy=Љ20x+80ЃЈ20ЁмxЁм40ЃЉЃЌЩшетжжНЁЩэЧђУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУжжНЁЩэЧђЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжНЁЩэЧђЕФЯњЪлЕЅМлВЛИпгк28дЊЃЌИУЩЬЕъЯњЪлетжжНЁЩэЧђУПЬьвЊЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃК
ЮвУЧжЊЕР![]() ЕФМИКЮвтвхЪЧдкЪ§жсЩЯЪ§
ЕФМИКЮвтвхЪЧдкЪ§жсЩЯЪ§![]() ЖдгІЕФЕугыдЕуЕФОрРыЃЌМД
ЖдгІЕФЕугыдЕуЕФОрРыЃЌМД![]() ЃЌвВОЭЪЧЫЕ
ЃЌвВОЭЪЧЫЕ![]() БэЪОдкЪ§жсЩЯЪ§
БэЪОдкЪ§жсЩЯЪ§![]() гыЪ§
гыЪ§![]() ЖдгІЕФЕужЎМфЕФОрРыЃЌетИіНсТлПЩвдЭЦЙуЮЊ
ЖдгІЕФЕужЎМфЕФОрРыЃЌетИіНсТлПЩвдЭЦЙуЮЊ![]() БэЪОЪ§жсЩЯ
БэЪОЪ§жсЩЯ![]() гы
гы![]() ЖдгІЕужЎМфЕФОрРыЃЎ
ЖдгІЕужЎМфЕФОрРыЃЎ
Р§1ЃКвбжЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
НтЃКШнвзПДГіЃЌдкЪ§жсЩЯгыдЕуОрРыЮЊ![]() ЕФЕуЕФЖдгІЪ§ЮЊ
ЕФЕуЕФЖдгІЪ§ЮЊ![]() КЭ
КЭ![]() ЃЌМД
ЃЌМД![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
Р§2ЃКвбжЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
НтЃКдкЪ§жсЩЯгы![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЕФЕуЕФЖдгІЪ§ЮЊ
ЕФЕуЕФЖдгІЪ§ЮЊ![]() КЭ
КЭ![]() ЃЌМД
ЃЌМД![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
ЗТеедФЖСВФСЯЕФНтЗЈЃЌЧѓЯТСаИїЪНжаЕФжЕЃЎ
ЃЈ1ЃЉ![]()
ЃЈ2ЃЉ![]()
ЃЈ3ЃЉгЩвдЩЯЬНЫїВТЯыЃКЖдгкШЮКЮгаРэЪ§![]() ЪЧЗёгазюаЁжЕЃПШчЙћгаЃЌаДГізюаЁжЕЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёгазюаЁжЕЃПШчЙћгаЃЌаДГізюаЁжЕЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌИје§ЮхБпаЮЕФЖЅЕувРДЮБрКХЮЊ![]() ЃЎШєДгФГвЛЖЅЕуПЊЪМЃЌбие§ЮхБпаЮЕФБпЫГЪБеыаазпЃЌЖЅЕуБрКХЕФЪ§зжЪЧМИЃЌОЭзпМИИіБпГЄЃЌдђГЦетжжзпЗЈЮЊвЛДЮЁАвЦЮЛЁБЃЎ
ЃЎШєДгФГвЛЖЅЕуПЊЪМЃЌбие§ЮхБпаЮЕФБпЫГЪБеыаазпЃЌЖЅЕуБрКХЕФЪ§зжЪЧМИЃЌОЭзпМИИіБпГЄЃЌдђГЦетжжзпЗЈЮЊвЛДЮЁАвЦЮЛЁБЃЎ
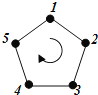
Шч:аЁгюЭЌбЇДгБрКХЮЊ![]() ЕФЖЅЕуПЊЪМЃЌЫћгІзп
ЕФЖЅЕуПЊЪМЃЌЫћгІзп![]() ИіБпГЄЃЌМДДг
ИіБпГЄЃЌМДДг![]() ЮЊЕквЛДЮЁАвЦЮЛЁБЃЌетЪБЫћЕНДяБрКХЮЊ
ЮЊЕквЛДЮЁАвЦЮЛЁБЃЌетЪБЫћЕНДяБрКХЮЊ![]() ЕФЖЅЕуЃЛШЛКѓДг
ЕФЖЅЕуЃЛШЛКѓДг![]() ЮЊЕкЖўДЮЁАвЦЮЛЁБЃЌЃЎЃЎЃЎЃЎШєаЁгюЭЌбЇДгБрКХЮЊ
ЮЊЕкЖўДЮЁАвЦЮЛЁБЃЌЃЎЃЎЃЎЃЎШєаЁгюЭЌбЇДгБрКХЮЊ![]() ЕФЖЅЕуПЊЪМЃЌдђЕкОХЪЎОХДЮЁАвЦЮЛЁБКѓЫћЫљДІЖЅЕуЕФБрКХЪЧЃЈ ЃЉ
ЕФЖЅЕуПЊЪМЃЌдђЕкОХЪЎОХДЮЁАвЦЮЛЁБКѓЫћЫљДІЖЅЕуЕФБрКХЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯACB=72ЁуЃЌНЋЁїABCШЦЕуBАДФцЪБеыЗНЯђа§зЊЕУЕНЁїBDEЃЈЕуDгыЕу AЪЧЖдгІЕуЃЌЕуEгыЕуCЪЧЖдгІЕуЃЉЃЌЧвБпDEЧЁКУОЙ§ЕуCЃЌдђЁЯABDЕФЖШЪ§ЮЊ

A. 36Ёу B. 40Ёу C. 45Ёу D. 50Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
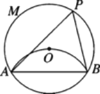
ЁОЬтФПЁПШчЭМЃЌдкдВЁбOжаЃЌНЋЛЁABбиЯвABелЕўЃЌЪЙЛЁABЧЁКУОЙ§дВаФOЃЌЕуPЪЧгХЛЁAMBЩЯвЛЕуЃЌдђЁЯAPBЕФЖШЪ§ЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
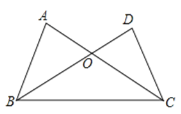
ЁОЬтФПЁПШчЭМЃЌЯТСаЬѕМўжаЃЌВЛФмжЄУїЁїABC Ёе ЁїDCBЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
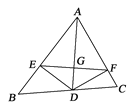
ЁОЬтФПЁПШчЭМЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDEЃЌDFЗжБ№ЪЧЁїABDКЭЁїACDЕФИпЃЌСЌНгEFНЛADгкG.ЯТСаНсТлЃКЂйADДЙжБЦНЗжEFЃЛЂкEFДЙжБЦНЗжADЃЛЂлADЦНЗжЁЯEDFЃЛЂмЕБЁЯBACЮЊ60ЁуЪБЃЌAG=3DGЃЌЦфжаВЛе§ШЗЕФНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com