
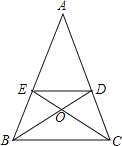
【题目】如图,在△ABC中,AB=AC,BD,CE分别是∠ABC,∠ACB的平分线,且DE∥BC,∠A=36°,则图中等腰三角形共有_____个.
【答案】12
【解析】
由已知条件,根据三角形内角和等于180、角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行找寻,注意做到由易到难,不重不漏.
解:∵AB=AC,∠A=36°,
∴△ABC是等腰三角形,∠ABC=∠ACB=![]() =72°,
=72°,
∵BD平分∠ABC,
∴∠EBD=∠DBC=36°,
∵ED∥BC,
∴∠AED=∠ADE=72°,∠EDB=∠DBC=36°,
∴在△ADE中,∠AED=∠ADE=72°,AD=AE,△ADE为等腰三角形,
在△ABD中,∠A=∠ABD=36°,AD=BD,△ABD是等腰三角形,
同理△AEC也是等腰三角形,
在△BED中,∠EBD=∠EDB=36°,ED=BE,△BED是等腰三角形,
同理△CED也是等腰三角形,
在△BDC中,∠BCD=∠BDC=72°,BD=BC,△BDC是等腰三角形,
同理△BEC也是等腰三角形,
∵∠OBC=∠OCB=∠ODE=∠OED=36°,
∴OD=OE,OB=OC,即△ODE,△OBC也为等腰三角形,
∵∠BEO=∠BOE=∠COD=∠ODC=72°,
∴CD=CO,BE=OB,
∴△CDO,△BOE也是等腰三角形,
所以共有12个等腰三角形.
故答案为:12.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
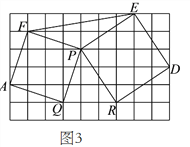
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,![]() 为原点,且满足
为原点,且满足![]() .
.
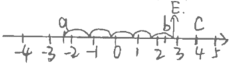
(1)![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)若![]() 的的中点为
的的中点为![]() .则点
.则点![]() 表示的数为__________;
表示的数为__________;
(3)小亮说“如果将点![]() 向右移动5个单位长度,得到点
向右移动5个单位长度,得到点![]() ,此时点
,此时点![]() 在原点的右侧,也在点
在原点的右侧,也在点![]() 的右侧”,他的说法正确吗?说明理由.
的右侧”,他的说法正确吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①
,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①![]() ;②FA平分
;②FA平分![]() ;③
;③![]() ;④
;④![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )
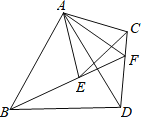
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
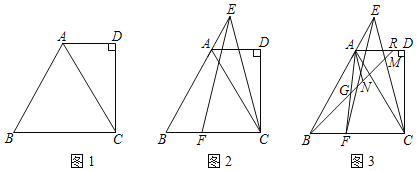
【题目】已知四边形ABCD中,AD∥BC,∠D=90°,AC平分∠BAD,∠ACD=30°
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点E在边BA的延长线上,在边BC上取一点F,连接EC、EF且EC=EF,求证:BF=AE;
(3)如图3,在(2)的条件下,连接AF,取AF的中点G,连接BG并延长交线段EC于M,交线段AD于R,过点A做AN∥EC交线段BR于N,若GN=2,EM=5,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点A (a,b),B(c,d),若点T(x,y)满足x=![]() ,y=
,y=![]() ,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
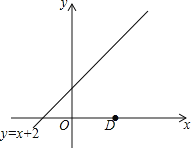
(1)若点E的纵坐标是6,则点T的坐标为 ;
(2)求点T (x,y)的纵坐标y与横坐标x的函数关系式:
(3)若直线ET交x轴于点H,当△DTH为直角三角形时,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com