
【题目】某文具店经销甲、乙两种不同的笔记本,已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,小玲同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时文具店获利最大?
【答案】(1)甲种笔记本的进价是6元/本,乙种笔记本的进价是4元/本;(2)购入甲种笔记本最多28本,此时获利最大
【解析】
(1)设甲种笔记本的进价为m元,乙种笔记本的进价为n元.根据王同学买4本甲种笔记本和3本乙种笔记本共用了47元,列出方程组即可解决问题.
(2)设购入甲种笔记本x本,根据购入这两种笔记本共60本,花费不超过296元,列出不等式求出x的取值范围;设利润为y元,根据题意得出y与x的函数关系式,再根据一次函数的性质解答即可.
(1)设甲种笔记本的进价为m元,乙种笔记本的进价为n元..
由题意得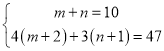 ,
,
解得![]() ,
,
答:甲种笔记本的进价是6元/本,乙种笔记本的进价是4元/本.
(2)设购入甲种笔记本x本,则购入乙种笔记本(60﹣x)本,
根据题意得6x+4(60﹣x)≤296,
解得n≤28,
设利润为y元,则y=2x+(60﹣x),
即y=x+60,
∵k=1>0,
∴y随x的增大而增大,
∴当x=28时文具店获利最大.
答:购入甲种笔记本最多28本,此时获利最大.


科目:初中数学 来源: 题型:
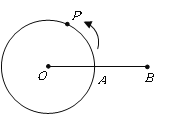
【题目】如图,![]() 是半径为
是半径为![]() 的
的![]() 上的定点,动点
上的定点,动点![]() 从
从![]() 出发,以
出发,以![]() 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点![]() 回到
回到![]() 地立即停止运动.
地立即停止运动.
(1)如果![]() ,求点
,求点![]() 运动的时间;
运动的时间;
(2)如果点![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() ,那么当点
,那么当点![]() 运动的时间为
运动的时间为![]() 时,判断直线
时,判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
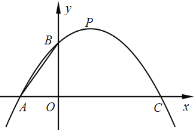
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
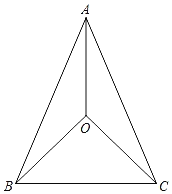
【题目】如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)求证:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
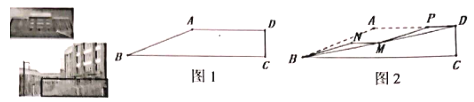
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图,![]() ,
,![]() ,楼梯
,楼梯![]() 的坡比为1:
的坡比为1:![]() ,为了增加楼梯的舒适度,将其改造成如图2,测量得
,为了增加楼梯的舒适度,将其改造成如图2,测量得![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 分别作
分别作![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,其中
,其中![]() 和
和![]() 为楼梯,
为楼梯,![]() 为平地,则平地
为平地,则平地![]() 的长度为_________
的长度为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
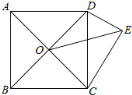
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
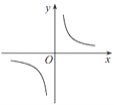
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.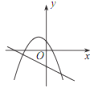 B.
B.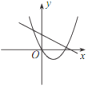 C.
C.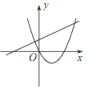 D.
D.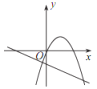
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
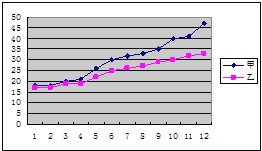
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差B.甲运动员得分的的中位数大于乙运动员得分的的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数D.甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com