
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=12$\sqrt{2}$cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动,同时,动点Q从点B出发沿BC方向以每秒$\sqrt{2}$cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为4. 分析 连接PP′交CQ于D,根据菱形的对角线互相垂直平分可得PP′⊥CQ,CD=DQ,用t表示出CD,过点P作PO⊥AC于O,可得四边形CDPO是矩形,再判断出△ABC是等腰直角三角形,根据等腰直角三角形的性质可得∠A=45°,从而得到△APO是等腰直角三角形,再用t表示出PO,然后根据矩形的对边相等列出方程求解即可.
解答 解: 解:如图,连接PP′交CQ于D,
解:如图,连接PP′交CQ于D,
∵四边形QPCP′为菱形,
∴PP′⊥CQ,CD=DQ,
∵点Q的速度是每秒1cm,
∴CD=$\frac{1}{2}$CQ=$\frac{1}{2}$(12$\sqrt{2}$-$\sqrt{2}$t)cm,
过点P作PO⊥AC于O,
则四边形CDPO是矩形,
∴CD=PO,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∴PO=$\frac{\sqrt{2}}{2}$AP,
∵点P的运动速度是每秒 2cm,
∴PO=$\frac{\sqrt{2}}{2}$×2t=$\sqrt{2}$tcm,
∴$\frac{1}{2}$(12$\sqrt{2}$-$\sqrt{2}$t)=$\sqrt{2}$t,
解得t=4,
故答案为4
点评 本题考查了翻折变换,菱形的判定与性质,等腰直角三角形的性质,作辅助线构造出矩形和等腰直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
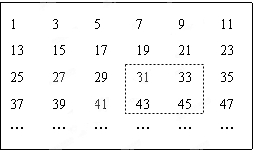 将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.
将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 速度(km/h) | 所走的路程(km) | 所用时间(h) | |
| 出发后第一小时内行驶 | x | x | 1 |
| 出发一小时以后行驶 | 1.5x | 180-x | $\frac{180-x}{1.5x}$ |
| 原计划行驶 | x | 180 | $\frac{180}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6a2b2=3ab•2ab | B. | -8x2+8x-2=-2(2x-1)2 | ||
| C. | 2x2+8x-1=2x(x+4)-1 | D. | a2-1=a(a-$\frac{1}{a}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com