
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
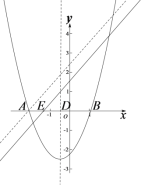
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①由二次函数的对称轴方程可得出答案;
②根据题意求出B点坐标为(2,0),代入抛物线解析式![]() 可得出答案;
可得出答案;
(2)求出E(-![]() ,0),点D的坐标为(-
,0),点D的坐标为(-![]() ,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-
,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-![]() ,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-
,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-![]() ,解出b<-2.
,解出b<-2.
解:(1)当![]() 时,
时,![]() 化为
化为![]() .
.
①![]() .
.
②∵抛物线的对称轴为直线![]() ,
,
∴点D的坐标为(-1,![]() ),OD=1.
),OD=1.
∵OB=2OD,
∴ OB=2.
∵点A,点B关于直线![]() 对称,
对称,
∴点B在点D的右侧.
∴ 点B的坐标为(![]() ,
,![]() ).
).
∵抛物线![]() 与x轴交于点B(
与x轴交于点B(![]() ,
,![]() ),
),
∴ ![]() .
.
解得![]() .
.
∴抛物线的表达式为![]() .
.
(2)设直线![]() 与x轴交点为点E,
与x轴交点为点E,
当y=0时,![]()
∴ ![]()
∴ E(![]() ,0).
,0).
抛物线的对称轴为![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).
①当![]() 时,
时,![]() .
.
∵OB=2OD,
∴ OB=b.
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(b,
),点B的坐标为(b,![]() ).
).
当![]() <
<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,

解得![]() .
.
②当![]() 时,
时,![]() .
.
∴ ![]() .
.
∵OB=2OD,
∴ OB=-b.
∵抛物线![]() 与x轴交于点A,B,且A在B的左侧,
与x轴交于点A,B,且A在B的左侧,
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(-b,
),点B的坐标为(-b,![]() ).
).
当0<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,
解得b<-2.
综上,b的取值范围是![]() 或
或![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
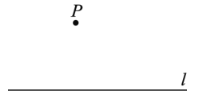
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,
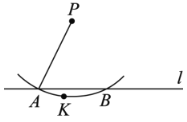
①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(不与
上(不与![]() 重合),将矩形沿
重合),将矩形沿![]() 折叠,使点
折叠,使点![]() 分别落在点
分别落在点![]() 处有下列结论:
处有下列结论:
①![]() 与
与![]() 互余;
互余;
②若![]() 平分
平分![]() 则
则![]()
③若直线![]() 经过点
经过点![]() 则
则![]()
④若直线![]() 交边
交边![]()
![]() 分别于
分别于![]() 当
当![]() 为等腰三角形时,五边形
为等腰三角形时,五边形![]() 的周长为
的周长为![]() .其中正确结论的序号是_____________________.
.其中正确结论的序号是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
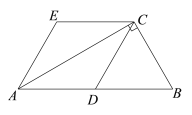
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图 90后从事互联网行业岗位分布图
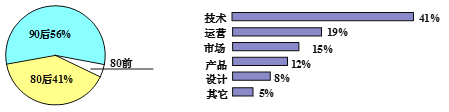
对于以下四种说法,你认为正确的是_____ (写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
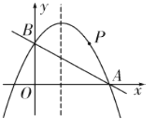
(1)求抛物线的解析式;
(2)若![]() 是抛物线上一点,且
是抛物线上一点,且![]() 点坐标为
点坐标为![]() ,点
,点![]() 为抛物线对称轴上一点,求
为抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)点![]() 为直线
为直线![]() 上的动点,点
上的动点,点![]() 为抛物线上的动点,当以点
为抛物线上的动点,当以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com