
【题目】阅读材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说
,也就是说![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离,这个结论可以推广为
对应的点之间的距离,这个结论可以推广为![]() 表示数轴上
表示数轴上![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:对于任何有理数![]() 是否有最小值?如果有,写出最小值;如果没有,请说明理由.
是否有最小值?如果有,写出最小值;如果没有,请说明理由.
 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】观察下面三行单项式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根据你发现的规律,解答下列问题:
(1)第①行的第8个单项式为 ;
(2)第②行的第9个单项式为 ;
(3)第③行的第n个单项式为 (用含n的式子表示);
(4)取每行的第8个单项式,令这三个单项式的和为A.
当![]() 时,求A的值.
时,求A的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
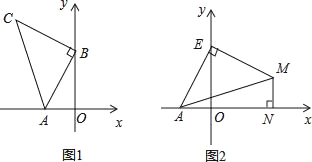
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:
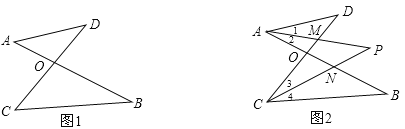
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十房”天然气正在紧张施工中,从2018年1月1日起居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.

(1)如果他家2018年全年使用300立方米天然气,那么需要交多少元天然气费?
(2)如果他家2018年全年使用500立方米天然气,那么需要交多少元天然气费?
(3)如果他家2018年需要交1563元天然气费,他家2018年用了多少立方米天然气?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com