
【题目】五·一”假期,某公司组织部分员工到A、B、C三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图,
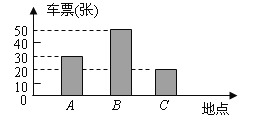
根据统计图回答下列问题:
(1)前往 A地的车票有_______ _张,前往C地的车票占全部车票的________%;
(2)若公司决定采用随机抽取的方式把车票分配给 100 名员工,在看不到车票的条下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 B 地车票的概率为___ ____;
(3)若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标数字1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李.”试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
【答案】(1)30;20.(2)50÷100=![]() (3)不公平.
(3)不公平.
【解析】
试题(1)考查了条形图的知识,解题的关键是识图;
(2)让去B地车票数除以车票总数即为所求的概率;
(3)此题考查了游戏公平性问题,解题的关键是求得小张得到车票的概率与小李得到车票的概率,只要相同就公平,否则就不公平.
试题解析:(1)30;20.
(2)50÷100=![]()
(3)不公平.
可能出现的所有结果列表如下:
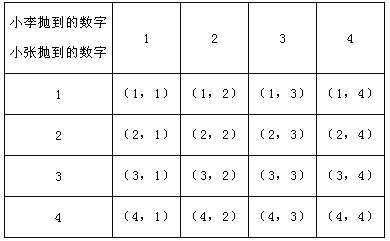
或画树状图如下:
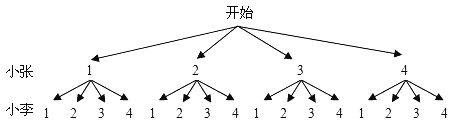
共有16种可能的结果,且每种的可能性相同,其中小张获得车票的结果有6种:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),
∴小张获得车票的概率为P=![]() ;则小李获得车票的概率为1-
;则小李获得车票的概率为1-![]() .
.
∴这个规则对小张、小李双方不公平.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】![]() 正方形
正方形![]() 与等腰直角三角形
与等腰直角三角形![]() 如图
如图![]() 所示重叠在一起,其中
所示重叠在一起,其中![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() 与
与![]() 全等吗?请说明理由.
全等吗?请说明理由.
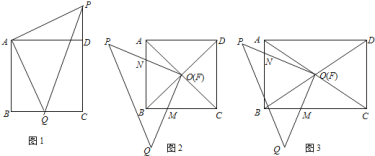
![]() 如图
如图![]() ,
,![]() 为正方形
为正方形![]() 对角线的交点,将一直角三角板
对角线的交点,将一直角三角板![]() 的直角顶点
的直角顶点![]() 与点
与点![]() 重合转动三角板使两直角边始终与
重合转动三角板使两直角边始终与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,使探索
,使探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
![]() 如图
如图![]() ,将
,将![]() 中的“正方形”改成“长方形”,其它的条件不变,且
中的“正方形”改成“长方形”,其它的条件不变,且![]() ,
,![]() ,
,![]() ,
,![]() ,试求
,试求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
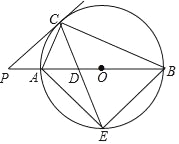
【题目】如图,AB是⊙O的直径,∠ACB的平分线交AB于点D,交⊙O于点E,过点C作⊙O的切线CP交BA的延长线于点P,连接AE.
(1)求证:PC=PD;
(2)若AC=5cm,BC=12cm,求线段AE,CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学本学期组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下:
小班名称 | 奥数 | 写作 | 舞蹈 | 篮球 | 航模 |
报名人数 | 215 | 201 | 154 | 76 | 65 |
小班名称 | 奥数 | 舞蹈 | 写作 | 合唱 | 书法 |
计划人数 | 120 | 100 | 90 | 80 | 70 |
若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
A. 奥数比书法容易 B. 合唱比篮球容易 C. 写作比舞蹈容易 D. 航模比书法容易
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1+y2 , 其中y1与x成反比例,y2与(x﹣2)成正比例.当x=1时,y=﹣1;x=3时,y=3.求:
(1)y与x的函数关系式;
(2)当x=﹣1时,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
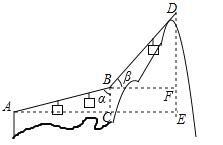
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现给出以下几个命题:
![]() 长度相等的两条弧是等弧;
长度相等的两条弧是等弧;![]() 相等的弧所对的弦相等;
相等的弧所对的弦相等;![]() 垂直于弦的直线平分这条弦并且平分弦所对的两条弧;
垂直于弦的直线平分这条弦并且平分弦所对的两条弧;![]() 钝角三角形的外接圆圆心在三角形外面;
钝角三角形的外接圆圆心在三角形外面;![]() 矩形的四个顶点必在同一个圆上.其中真命题的个数有( )
矩形的四个顶点必在同一个圆上.其中真命题的个数有( )
A. 1 个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1,x2是方程的两个实数根,且x12+x22=4,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com