
【题目】某商家为迎接“10周年购物狂欢节”,准备将编号为l号,2号,…,60号的奖券分别对应60份奖品.现将奖券不均匀分配放置在![]() ,
,![]() ,
,![]() 三个抽奖盒中,若将
三个抽奖盒中,若将![]() 盒中的26号奖券调换到
盒中的26号奖券调换到![]() 盒,将
盒,将![]() 盒中的44号奖券调换到
盒中的44号奖券调换到![]() 盒,此时,
盒,此时,![]() 、
、![]() 两盒奖券的编号平均数比调换前增加了0.6,
两盒奖券的编号平均数比调换前增加了0.6,![]() 盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,
盒奖券的编号平均数比调换前增加了0.9,同时经计算发现,![]() 盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前
盒中编号平均数调换前低于36,调换后编号平均数却高于36,则调换前![]() 盒中有_________张奖券.
盒中有_________张奖券.
【答案】24
【解析】
设调换前A盒中有x张奖券,编号平均数为a,B盒中有y张奖券,编号平均数为b,C盒中有z张奖券,编号平均数为c,利用B盒中平均数增加了0.9可求出B盒中的奖券数,再根据A、C盒中的编号平均数增加0.6建立等式,根据B盒中编号平均数调换前低于36,调换后编号平均数却高于36,可得出B盒中编号数的总和范围,进而得到A、C盒中编号数的范围,从而建立不等式求解.
设调换前A盒中有x张奖券,编号平均数为a,B盒中有y张奖券,编号平均数为b,C盒中有z张奖券,编号平均数为c,
由题意可得:![]() ,
,![]()
∵调换后B盒中平均数增加了0.9
∴![]() ,解得
,解得![]()
∵![]() 盒中编号平均数调换前低于36,调换后编号平均数却高于36
盒中编号平均数调换前低于36,调换后编号平均数却高于36
∴调换前B盒中的编号平均数![]()
则调换前B盒中的编号总和范围:![]()
∵调换后![]() 、
、![]() 两盒奖券的编号平均数比调换前增加了0.6
两盒奖券的编号平均数比调换前增加了0.6
∴![]() ,
,![]()
整理得![]() ,
,![]()
∵![]() ,即
,即![]()
∴![]() ,整理得
,整理得![]()
由调换前,![]() ,
,![]() 可得:
可得:
![]() ,即
,即![]()
将![]() ,
,![]() ,
,![]() 代入
代入![]() 得:
得:
![]()
整理得:![]()
解得![]()
∵![]() 为正整数,
为正整数,
∴![]()
即调换前A盒中有24张奖券,
故答案为:24.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
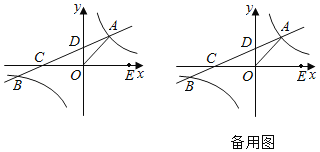
(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
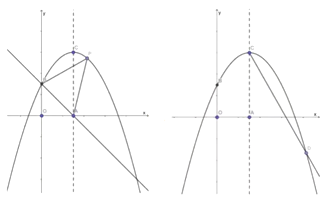
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,
,![]() .当
.当![]() 最长时,求
最长时,求![]() 的最小值;
的最小值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,将
,将![]() 沿直线
沿直线![]() 平移得到
平移得到![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿边
沿边![]() 翻折得
翻折得![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求此时点
是等腰三角形时,求此时点![]() 的坐标.
的坐标.
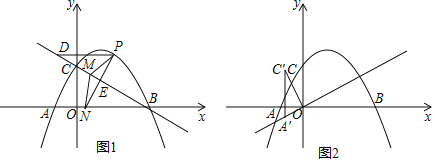
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
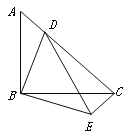
(1)求∠DCE的度数;
(2)当AB=4,AD∶DC=1∶3时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
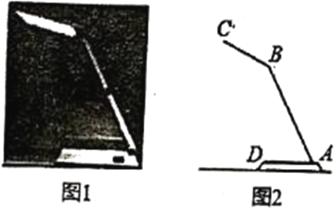
【题目】如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂![]() 长为
长为![]() 灯翠
灯翠![]() 长为
长为![]() ,底座
,底座![]() 厚度为
厚度为![]() 根据使用习惯,灯臂
根据使用习惯,灯臂![]() 的倾斜角
的倾斜角![]() 固定为
固定为![]() ,
,
(1)当![]() 转动到与桌面平行时,求点
转动到与桌面平行时,求点![]() 到桌面的距离;
到桌面的距离;
(2)在使用过程中发现,当![]() 转到至
转到至![]() 时,光线效果最好,求此时灯罩顶端
时,光线效果最好,求此时灯罩顶端![]() 到桌面的高度(参考数据:
到桌面的高度(参考数据:![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.该函数的图象的开口向下B.该函数图象的顶点坐标是![]()
C.当![]() 时,
时,![]() 随
随![]() 的增大而增大D.该函数的图象与
的增大而增大D.该函数的图象与![]() 轴有两个不同的交点
轴有两个不同的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com