
����Ŀ����ͼ����֪������![]() ����������
����������![]() ��
��![]() �ᷭ�ۣ��õ�������
�ᷭ�ۣ��õ�������![]() ��
��
��1�����������![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���ֽ�������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ
����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ![]() ����
����![]() ��Ľ������������Ϊ
��Ľ������������Ϊ![]() ��
��![]() ����������
����������![]() ����Ҳƽ��
����Ҳƽ��![]() ����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ
����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ![]() ����
����![]() �ύ�����������Ϊ
�ύ�����������Ϊ![]() ��
��![]() ����ƽ�ƹ����У��Ƿ�����Ե�
����ƽ�ƹ����У��Ƿ�����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��ε����Σ������ڣ��������ʱ
Ϊ������ı����Ǿ��ε����Σ������ڣ��������ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
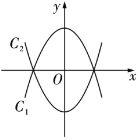

���𰸡���1��![]() ����2�����ڣ���
����2�����ڣ���![]() ʱ���Ե�
ʱ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ�
Ϊ������ı����Ǿ��Σ�
��������
��1�������߷���ǰ�����x��Գƣ�a��Ϊ�෴����
��2������AN��NE��EM��MA��M��N����ԭ��O�Գ�OM��ON��A��E����ԭ��O�Գ�OA��OE���ж��ı���ANEMΪƽ���ı��Σ���AM2��ME2��AE2�����m��3��������⣮
�⣺��1����������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��
��
����![]() �ᷭ�ۺ������Ϊ
�ᷭ�ۺ������Ϊ![]() ��
��
��������![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ��
��
��2�����ڣ�
���ɣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��������ɵã�
��������ɵã�![]() ��
��![]() ��
��
��![]() ��
��![]() ����ԭ��
����ԭ��![]() �Գƣ���
�Գƣ���![]() ��
��
ԭ![]() ��
��![]() ��������
��������![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ����ԭ��
����ԭ��![]() �Գƣ���
�Գƣ���![]() ��
��
���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
��ʱ![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
����![]() ʱ���Ե�
ʱ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ�
Ϊ������ı����Ǿ��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
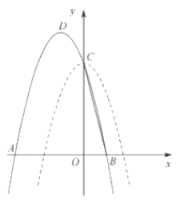
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
Ϊ��![]() �ϵ�һ��������
�ϵ�һ��������![]() ��
��![]() �غϣ��㣬��
�غϣ��㣬��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��

��1����գ�![]() ______��
______��![]() ______��
______��
��2����![]() ʱ��֤����
ʱ��֤����![]() ��
��
��3��![]() �������Сֵ��_______��
�������Сֵ��_______��
��4����![]() ��������
��������![]() ���ⲿʱ��ֱ��д��
���ⲿʱ��ֱ��д��![]() �ķ�Χ______��
�ķ�Χ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
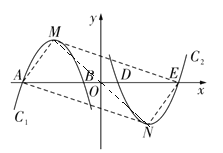
����Ŀ����ͼ����������![]() ƽ�ƺ��������߾���ԭ�����ߵĶ���
ƽ�ƺ��������߾���ԭ�����ߵĶ���![]() ������������
������������![]() �������ύ�ڵ�
�������ύ�ڵ�![]() ������
������![]() ��
��![]() ��������������
��������������![]() �����һ������
�����һ������![]() ���������ߵĶ�����
���������ߵĶ�����![]() .
.
��1�����![]() �����ꣻ
�����ꣻ
��2�����![]() �����������ϣ�����
�����������ϣ�����![]() �����
�����![]() ƽ��
ƽ��![]() �����
�����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£���������![]() ��
��![]() ������ƽ�ƣ���
������ƽ�ƣ���![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() ��
��![]() ����ʱ����ֱ��д��ƽ�ƺ�õ������ߵı���ʽ.
����ʱ����ֱ��д��ƽ�ƺ�õ������ߵı���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӽ�����ij���о��꼶1200��ѧ�������ѡȡһ����ѧ�����е��飬���������A������ʱ����1Сʱ��B��1Сʱ������ʱ����4Сʱ��C��4Сʱ������ʱ����7Сʱ��D������ʱ�䣾7Сʱ��ͳ�ƽ���Ƴ�����ͼͳ��ͼ�����½�������ȷ�ĸ����ǣ� ��
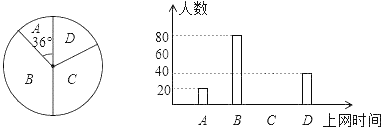
�ٲμӵ����ѧ����200�ˣ�
�ڹ���У����������7Сʱ��ѧ��������900��
��C��������60�ˣ�
��D���Ե�Բ�Ľ���72����
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ(��1��3)��(��4��1)��(��2��1)���Ƚ���ABC��һȷ������ƽ�Ƶõ���A1B1C1����B�Ķ�Ӧ��B1��������(1��2)���ٽ���A1B1C1��ԭ��O˳ʱ����ת90���õ���A2B2C2����A1�Ķ�Ӧ��Ϊ��A2��
��1��������A1B1C1�͡�A2B2C2��
��2������������α任�����У���A������A1����A2��·���ܳ���
��3�����߶�B1C1��ת��B2C2��ɨ����ͼ�ε������
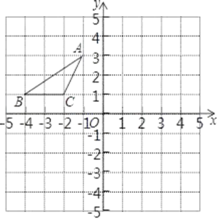
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹��������ܱߵ�ũ����ֲ˵Ļ����ԣ�ij��˾�ƻ��½�![]() ��
��![]() ��������80���������۸�ũ���ֲˣ���֪��1��
��������80���������۸�ũ���ֲˣ���֪��1��![]() �����Һ�2��
�����Һ�2��![]() ������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
|
| |
�ɱ�����Ԫ/���� | 2.5 |
|
���ۼۣ���Ԫ/���� | 3.1 | 3.5 |
��1����![]() ��ֵ��
��ֵ��
��2����֪�½�![]() �����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�
�����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��ͼ�����ͬһ����ֱ��·�ϣ��״�ѧУȥͼ��ݣ��Ҵ�ͼ��ݻ�ѧУ���ס������˶����ٲ�����ͬʱ���������ȵ���Ŀ�ĵأ�����֮��ľ���y���ף���ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ��

��1������ͼ����Ϣ����t���� ������ʱ�����������������ٶ�Ϊ�� ����/���ӣ��ҵ��ٶ�Ϊ�� ����/���ӣ�
��2��ͼ�е�A������Ϊ�� ����
��3�����߶�AB��ֱ�ߵĺ�������ʽ��
��4�������������У���ʱ�������400�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ͼ2���ڡ�ABC�У�AB��13��BC��14��![]() .
.
̽������ͼ1��AH��BC�ڵ�H����AH��___��AC��___����ABC�����![]() ��___.
��___.
��չ����ͼ2����D��AC�ϣ������A��C�غϣ����ֱ����A��C��ֱ��BD�Ĵ��ߣ�����ΪE��F����BD��x��AE��m��CF��n��������D��A�غ�ʱ��������Ϊ![]() ��0��.
��0��.
��1���ú�x��m��n�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��
��2����(m+n)��x�ĺ�����ϵʽ������(m+n)�����ֵ����Сֵ��
��3���Ը�����һ��xֵ����ʱֻ��ȷ��Ψһ�ĵ�D��ָ��������x��ȡֵ��Χ.
���֣�����ȷ��һ��ֱ�ߣ�ʹ��A��B��C���㵽����ֱ�ߵľ���֮����С������д�����̣�����д�������Сֵ.
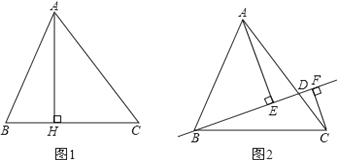
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ͼ2����ԲO�У�![]() ��
��![]() ������AB�뻡AB��Χ�ɵĹ���
������AB�뻡AB��Χ�ɵĹ���![]() �����߽����Ӱ����
�����߽����Ӱ����![]() �Ƶ�B˳ʱ����ת
�Ƶ�B˳ʱ����ת![]() ��
��![]() ����A�Ķ�Ӧ����
����A�Ķ�Ӧ����![]() ��
��
![]() ��O���߶�AB�ľ�����______��
��O���߶�AB�ľ�����______��![]() ______
______![]() ����O������Ӱ����
����O������Ӱ����![]() �����߽�
�����߽�![]() ʱ��
ʱ��![]() ��ȡֵ��Χ��______��
��ȡֵ��Χ��______��
![]() ��ͼ3���߶�B���Ż�ACB�Ľ�����D����
��ͼ3���߶�B���Ż�ACB�Ľ�����D����![]() ʱ��˵����D��AO���ӳ����ϣ�
ʱ��˵����D��AO���ӳ����ϣ�
![]() ��ֱ��
��ֱ��![]() ��ԲO����ʱ����
��ԲO����ʱ����![]() ��ֵ�����ʱ��
��ֵ�����ʱ��![]() �˶�·���ij��ȣ�
�˶�·���ij��ȣ�
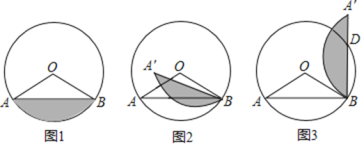
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com