Question

已知直线y=kx+6与直线y=2x相交于点P（m，4），与x轴相交于点A．
（1）求点P和点A的坐标；
（2）若点B（x，y）是线段PA上一个动点（A点除外），设△OAB的面积为S．求S关于x的函数关系式以及自变量x的取值范围．

Answer 1

解：（1）把P（m，4）代入y=2x得4=2m，解得m=2，如图，
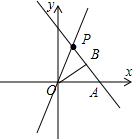
所以P点坐标为（2，4），
把P（2，4）代入y=kx+6得4=2k+6，解得k=-1，
所以y=-x+6，
令y=0，则-x+6=0，解得x=6，
所以点A的坐标为（0，6）；

（2）∵点B（x，y）是线段PA上一个动点（A点除外），
∴4≤x＜6，
S=OA•y
=•6•（-x+6）
=-3x+18，
∴S关于x的函数关系式为y=-3x+18（4≤x＜6）．
分析：（1）先把P（m，4）代入y=2x可求出m，确定P点坐标，再把P（2，4）代入y=kx+6可求出k的值得到以y=-x+6，然后把y=0代入可计算出对应的x的值，从而确定A点坐标；
（2）由于点B（x，y）是线段PA上一个动点（A点除外）得到4≤x＜6，根据三角形面积公式得到S=OA•y，然后把y=-x+6代入，再整理即可．
点评：本题考查了两直线平行或相交的问题：直线y=k₁x+b₁（k₁≠0）和直线y=k₂x+b₂（k₂≠0）平行，则k₁=k₂；若直线y=k₁x+b₁（k₁≠0）和直线y=k₂x+b₂（k₂≠0）相交，则交点坐标满足两函数的解析式．也考查了待定系数法求函数的解析式．