
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
【答案】(1)50°;(2)详见解析;(3)![]()
【解析】
(1)连接BD,如图,利用切线性质和圆周角定理得到∠ADG=∠ABD=90°,再利用等角的余角相等得到∠ADB=∠G=50°,然后根据圆周角定理得到∠ACB的度数;
(2)连接CD,如图,利用等腰三角形的性质得到∠ABE=∠AEB,∠ODC=∠OCD,再利用圆周角定理得到∠ABC=∠ADC,然后根据三角形内角和可判断∠BAD=∠DOC;
(3)先证明△ABD∽△OFC得到![]() ,设
,设![]() 则
则![]() 则利用三角形面积公式得到
则利用三角形面积公式得到![]() 则可设OF=4k,则OA=5k,利用勾股定理计算出CF,然后根据正切的定义求解.
则可设OF=4k,则OA=5k,利用勾股定理计算出CF,然后根据正切的定义求解.
(1)解:连接BD,如图,
∵DG为切线,
∴AD⊥DG, ∴∠ADG=90°,
∵AD为直径, ∴∠ABD=90°,
![]() ∠GDB+∠G=90°,∠ADB+∠GDB=90°,
∠GDB+∠G=90°,∠ADB+∠GDB=90°,
∴∠ADB=∠G=50°,
∴∠ACB=∠ADB=50°;
(2)证明:连接CD,如图,
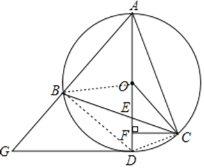
∵AB=AE, ∴∠ABE=∠AEB,
∵OD=OC, ∴∠ODC=∠OCD,
而∠ABC=∠ADC, ∴∠ABE=∠AEB=∠ODC=∠OCD,
∴∠BAD=∠FOC;
(3)解:∵∠BAD=∠FOC,∠ABD=∠OFC,
∴△ABD∽△OFC,
∴![]() ,
,
∵ ![]()
设![]() 则
则![]()
∴![]()
∴![]()
∵![]()
∴设OF=4k,则OA=5k,
在Rt△OCF中,OC=5k, CF=![]()
∴tan∠CAF=![]()


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.

已知:如图,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() ,使直线
,使直线![]() 直线
直线![]() .
.
作法:如图,
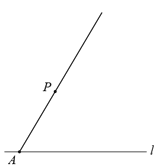
①在直线![]() 上任取一点
上任取一点![]() ,作射线
,作射线![]() ;
;
②以![]() 为圆心,
为圆心,![]() 为半径作弧,交直线
为半径作弧,交直线![]() 于点
于点![]() ,连接
,连接![]() ;
;
③以![]() 为圆心,
为圆心,![]() 长为半径作弧,交射线
长为半径作弧,交射线![]() 于点
于点![]() ;分别以
;分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,在
长为半径作弧,在![]() 的右侧两弧交于点
的右侧两弧交于点![]() ;
;
④作直线![]() ;
;
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依据1).
.(_______________________________)(填依据1).
![]() ,
,
![]() .
.
![]() ,∴直线
,∴直线![]() 直线
直线![]() .(______________________)(填依据2).
.(______________________)(填依据2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为顶点,
为顶点,![]() 为抛物线上一动点(与点
为抛物线上一动点(与点![]() 不重合)
不重合)
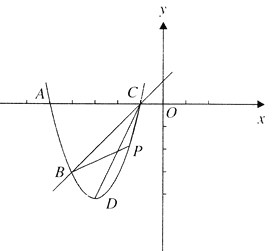
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
![]() 该抛物线上是否存在点
该抛物线上是否存在点![]() ,使
,使![]() ?若存在,求出所有点
?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划今年养殖无公害标准化龙虾和鲤鱼,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表:(单位:千元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
鲤鱼 | 9 | 3 | 30 |
龙虾 | 4 | 10 | 20 |
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.设鲤鱼种苗的投放量为x吨.
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了______分钟.
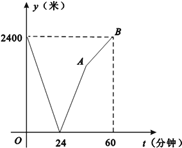
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月“停课不停学”期间,某校采用简单随机抽样的方式调查本校学生参加第一天线上学习的时长,将收集到的数据制成不完整的频数分布表和扇形图,如下所示:
组别 | 学习时长(分钟) | 频数(人) |
第1组 | x≤40 | 3 |
第2组 | 40<x≤60 | 6 |
第3组 | 60<x≤80 | m |
第4组 | 80<x≤100 | 18 |
第5组 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)学校有学生2400人,学校决定安排老师给““线上学习时长”在x≤60分钟范围内的学生打电话了解情况,请你根据样本估计学校学生“线上学习时长”在x≤60分钟范围内的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
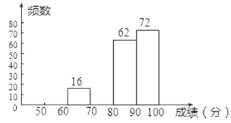
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() .为了研究图中线段之间的数量关系,设
.为了研究图中线段之间的数量关系,设![]() .
.
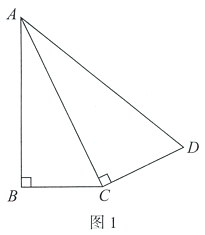
(1)由题意可得![]() ,(在括号内填入图1中相应的线段)y关于x的函数表达式为
,(在括号内填入图1中相应的线段)y关于x的函数表达式为![]() ________;
________;
(2)如图2,在平面直角坐标系![]() 中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
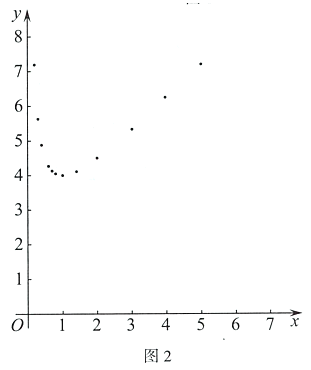
(3)结合函数图象,解决问题:
①写出该函数的一条性质:__________________________;
②估计![]() 的最小值为__________.(结果精确到0.1)
的最小值为__________.(结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校对八年级![]() 班的体育成绩做了模拟测评,将各个班的满分人数绘制成两幅不完整的统计图(如图):
班的体育成绩做了模拟测评,将各个班的满分人数绘制成两幅不完整的统计图(如图):
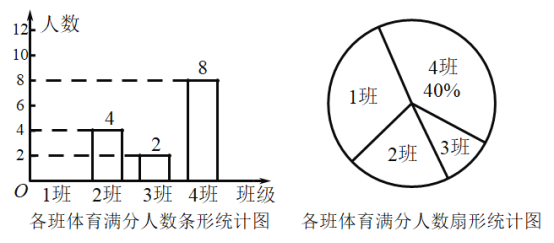
根据图中信息解答以下问题:
(1)扇形统计图中,“![]() 班”所在扇形的圆心角是 度,并补全条形统计图;
班”所在扇形的圆心角是 度,并补全条形统计图;
(2)班满分同学中有![]() 名(其中
名(其中![]() 女
女![]() 男)的跳远动作十分标准,
男)的跳远动作十分标准,![]() 班班主任准备从这名同学中任选
班班主任准备从这名同学中任选![]() 名给本班同学示范,请利用画树状图或列表的方法求出选出名同学恰好是一男一女的概率.
名给本班同学示范,请利用画树状图或列表的方法求出选出名同学恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com