
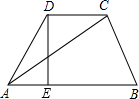
 如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.
如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$. 分析 作CF⊥AB,设AE=x,根据勾股定理求出DE,在Rt△ACF中,根据勾股定理列出方程,解方程求出x的值,得到答案.
解答 解: 作CF⊥AB于F,
作CF⊥AB于F,
设AE=x,
∵∠DAE=60°,
∴∠ADE=30°,
∴AD=2x,由勾股定理得,DE=$\sqrt{3}$x,
由题意得,四边形DEFC是矩形,
∴CF=DE=$\sqrt{3}$x,EF=CD=2,AF=x+2,
在Rt△ACF中,AC2=CF2+AF2,
即19=($\sqrt{3}$x)2+(x+2)2,
解得x1=$\frac{3}{2}$,x2=-$\frac{5}{2}$(舍去),
DE=$\sqrt{3}$x=$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查的是梯形的性质,灵活运用梯形的性质、直角三角形的性质和勾股定理是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
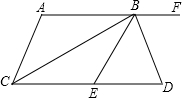 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.
如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
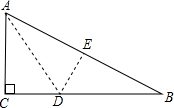 如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 5cm | C. | 3$\sqrt{5}$cm | D. | 9$\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
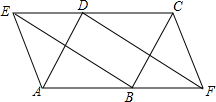 如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF
如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com