
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上,AB与x轴交于点E,BE:AE=1:2.若点B的坐标为(-2,1),则k的值为________.
的图象上,AB与x轴交于点E,BE:AE=1:2.若点B的坐标为(-2,1),则k的值为________.
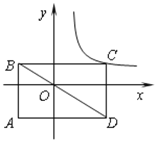
【答案】3
【解析】
根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形AEOF=S四边形HCGO,根据反比例函数比例系数的几何意义即可求出k+1=4,再解出k的值即可.
解:如图:∵BE:AE=1:2.点B的坐标为(-2,1),
∴点A的坐标为(-2,-2)
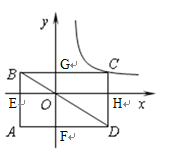
∵四边形ABCD、FAEO、OEBG、GOHC为矩形,
又∵BO为四边形GBEO的对角线,OD为四边形OHDF的对角线,
∴S△BEO=S△BGO,S△OFD=S△OHD,S△CBD=S△ADB,
∴S△CBDS△BEOS△OFD=S△ADBS△BGOS△OHD,
∴S四边形HCGO=S四边形AEOF=2×2=4,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴xy=k+1,
∴k+1=4
解得k=3


科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
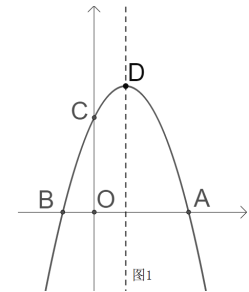
(1)求![]() 的值及顶点
的值及顶点![]() 的坐标;
的坐标;
(2)如图1,若动点![]() 在第一象限内的抛物线上,动点
在第一象限内的抛物线上,动点![]() 在对称轴
在对称轴![]() 上,当
上,当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
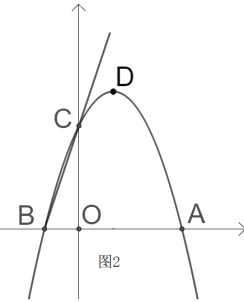
(3)如图2,若点![]() 是二次函数图像上对称轴右侧一点,设点
是二次函数图像上对称轴右侧一点,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,到抛物线的对称轴的距离为
,到抛物线的对称轴的距离为![]() ,当
,当![]() 时,请求出点
时,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“我为武汉加油”征文活动中,学校计划对获得一、二等奖的学生分别奖励一台计算器,一个考试包.已知购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元,购买
元,购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元.
元.
(1)计算器、考试包的单价分别为多少元?
(2)经与商家协商,购买计算器超过![]() 台时,每增加一台,单价降低
台时,每增加一台,单价降低![]() 元;超过
元;超过![]() 台,均按购买
台,均按购买![]() 台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计
台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计![]() 人,其中一等奖的人数不少于
人,其中一等奖的人数不少于![]() 人,且不超过
人,且不超过![]() 人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
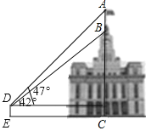
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果精确到0.1m).参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为![]() ,看房屋底部D处的俯角为
,看房屋底部D处的俯角为![]() ,石榴树与该房屋之间的水平距离为
,石榴树与该房屋之间的水平距离为![]() 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,过点B作BD⊥AC于点D,BE平分∠ABD交AC于点E.

(1)求证:CB=CE;
(2)若∠CEB=80°,求∠DBC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
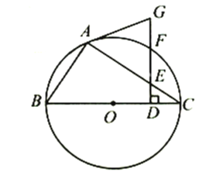
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com