
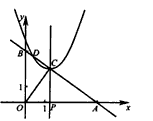
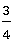 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2)。
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2)。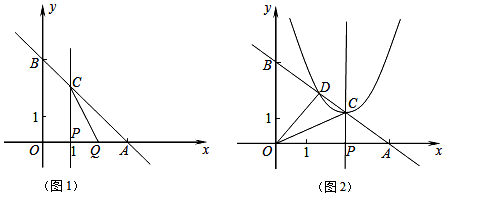
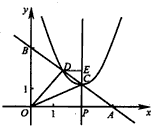
| 解:(1)①C(1,2),Q(2,0); ②由题意得:P(t,0),C(t,-t+3),Q(3-t,0), 分两种情况讨论: 情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°, ∴CQ⊥OA, ∵CP⊥OA, ∴点P与点Q重合,OQ=OP, 即3-t=t, ∴t=1.5; 情形二:当△AQC∽△AOB时,∠ACQ=∠AOB=90°, ∵OA=OB=3, ∴△AOB是等腰直角三角形, ∴△ACQ也是等腰直角三角形, ∵CP⊥OA, ∴AQ=2CP, 即t=2(-t+3), ∴t=2, ∴满足条件的t的值是1.5秒或2秒; |
|
(2)①由题意得:C(t,-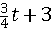 ) ) ∴以C为顶点的抛物线解析式是y= 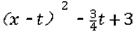 , ,由 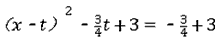 , ,解得 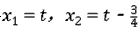 , ,过点D作DE⊥CP于点E, 则∠DEC=∠AOB=90°, ∵DE∥OA, ∴∠EDC=∠OAB, ∴△DEC∽△AOB ∴ 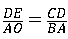 ∵AO=4,AB=5,DE= 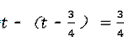 ∴CD= 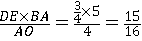 ; ;②∵ 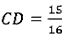 , ,CD边上的高= 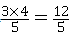 , ,∴ 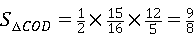 , ,∴S△COD为定值, 要使OC边上的高h的值最大,只要OC最短, 因为当OC⊥AB时OC最短, 此时OC的长为 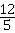 ,∠BCO=90° ,∠BCO=90°∵∠AOB=90° ∴∠COP=90°-∠BOC=∠OBA 又∵CP⊥OA ∴Rt△PCO∽Rt△OAB ∴ 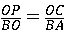 ,OP= ,OP=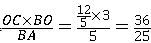 , ,即t= 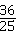 ∴当t为 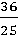 秒时,h的值最大。 秒时,h的值最大。 |
  |


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
| 4 |
| 27 |
| 22 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com