
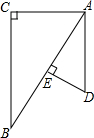
 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )| A. | $\frac{AC}{DE}$=$\frac{AB}{AD}$ | B. | ∠B=∠D | C. | AD∥BC | D. | ∠BAC=∠D |
分析 根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
解答 解:∵∠C=∠AED=90°,$\frac{AC}{DE}$=$\frac{AB}{AD}$,
∴△ABC∽△DAE,故选项A可以证明相似;
∵∠C=∠AED=90°,∠B=∠D,
∴△ABC∽△ADE,故B选项错误;
∵AD∥BC,
∴∠B=∠DAE,
∵∠C=∠AED=90°,
∴△ABC∽△DAE,故选项C可以证明相似;
∵∠BAC=∠D,∠C=∠AED=90°,
∴△ABC∽△DAE,故选项D可以证明相似;
故选B.
点评 本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
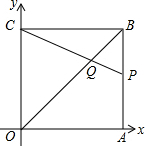 如图,正方形OABC的边长为6,顶点A,C在坐标轴上,点P在AB上,CP交OB于点Q,S△BPQ=$\frac{1}{4}$S△OQC,则点Q的坐标为(4,4).
如图,正方形OABC的边长为6,顶点A,C在坐标轴上,点P在AB上,CP交OB于点Q,S△BPQ=$\frac{1}{4}$S△OQC,则点Q的坐标为(4,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-ab2)3÷(ab2)2=-ab2 | B. | 3a+2a=5a2 | C. | (2a+b)(2a-b)=2a2-b2 | D. | (2a+b)2=4a2+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
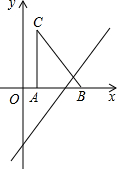 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com