
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
⑴ 分别以点![]() (1,0),
(1,0),![]() (1,1),
(1,1),![]() (3,2)为圆心,1为半径作圆,得到⊙
(3,2)为圆心,1为半径作圆,得到⊙![]() ,⊙
,⊙![]() 和⊙
和⊙![]() ,其中是
,其中是![]() 的角内圆的是 ;
的角内圆的是 ;
⑵ 如果以点![]() (
(![]() ,2)为圆心,以1为半径的⊙
,2)为圆心,以1为半径的⊙![]() 为
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
⑶ 点![]() 在第一象限内,如果存在一个半径为1且过点
在第一象限内,如果存在一个半径为1且过点![]() (2,
(2,![]() )的圆为
)的圆为![]() 的角内相切圆,直接写出
的角内相切圆,直接写出![]() 的取值范围.
的取值范围.
【答案】(1) ⊙B,⊙C;(2) ![]() ;(3) 60°≤∠EOM<90°.
;(3) 60°≤∠EOM<90°.
【解析】
(1)画出图象,根据角内相切圆的定义判断即可.
(2)求出两种特殊位置时t的值即可判断.
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点![]() 的圆为∠EOM的角内相切圆.
的圆为∠EOM的角内相切圆.
⑴ 如图1中,![]() 点
点![]() (1,0),
(1,0),![]() (1,1),
(1,1),![]() (3,2)
(3,2)
![]() 观察图象可知,⊙B和⊙C是∠EOF的角内圆.
观察图象可知,⊙B和⊙C是∠EOF的角内圆.
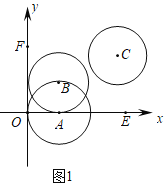
故答案为:⊙B,⊙C;
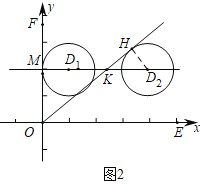
⑵ 如图,当⊙![]() 与
与![]() 轴相切时,设切点为
轴相切时,设切点为![]() ,则
,则![]() ,可得
,可得![]() .
.
当⊙![]() 与
与![]() 相切时,设切点为
相切时,设切点为![]() ,连接
,连接![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,
由![]() 的性质得:
的性质得:![]()
![]()
则△![]() ,△
,△![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
可得![]() ,
,
可知,满足条件的![]() 的取值范围是
的取值范围是![]() .
.
⑶如图3中,连接OP,OM.
∵![]() ,
,
∴![]()
∴∠POE=60°,
观察图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,
存在一个半径为1且过点![]() 的圆为∠EOM的角内相切圆,
的圆为∠EOM的角内相切圆,
∴ 60°≤∠EOM<90°.



科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 边的中点.将
边的中点.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
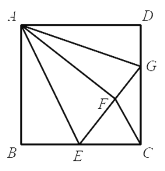
A.①②B.①③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节前夕“新型冠状病毒”爆发.疫情就是命令,防控就是使命,全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.如图两幅图是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
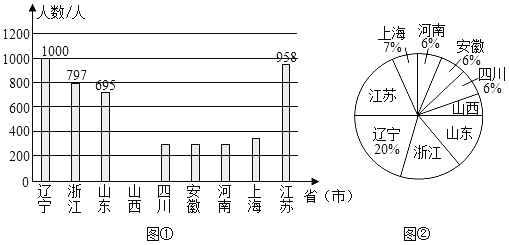
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为 人;
②请将图①的条形统计图补充完整;
(2)请求出图②的扇形统计图中“山西”所对应扇形的圆心角的度数;
(3)本次河北驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
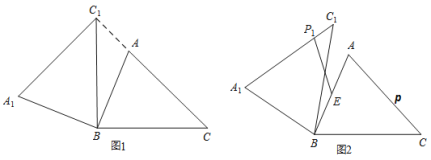
按逆时针方向旋转,得到![]() .(1)如图1,当点
.(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,则
的延长线上时,则![]() 的度数为______________度;(2)如图2,点
的度数为______________度;(2)如图2,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,则线段
,则线段![]() 长度最小值是_____________.
长度最小值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() (顶点是网格线的交点)和直线l及点O.
(顶点是网格线的交点)和直线l及点O.
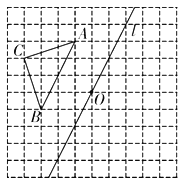
(1)画出![]() 关于直线l对称的
关于直线l对称的![]() ;
;
(2)连接OA,将OA绕点O顺时针旋转![]() ,画出旋转后的线段;
,画出旋转后的线段;
(3)在旋转过程中,当OA与![]() 有交点时,旋转角
有交点时,旋转角![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
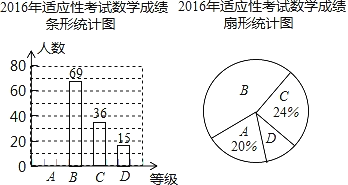
【题目】某校为了解九年级学生2020年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图.请根据统计图中的信息解答下列问题:
(1)此次抽查的学生人数为 ;
(2)把条形统计图和扇形统计图补充完整;
(3)若该校九年级有学生1200人.请估计在这次适应性考试中达到B等级以上(含B等级)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为 ![]() 的产品为合格),随机各抽取了
的产品为合格),随机各抽取了 ![]() 个样品进行检测,过程如下: 收集数据(单位:
个样品进行检测,过程如下: 收集数据(单位:![]() ):
):
甲车间:![]()
乙车间:![]()
整理数据(表 1):
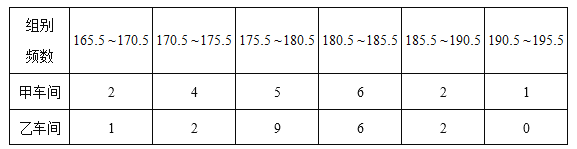
分析数据(表 2):

应用数据:
(1)直接写出表 2 中的 ![]() ,
, ![]() ;
;
(2)估计甲车间生产的 ![]() 个该款新产品中合格产品有多少个?
个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸是一种许多人熟悉的活动.近些年,经过许多人的努力,已经找到了多种将正方形折纸的一边三等分的精确折法,下面探讨其中的一种折法:
(综合与实践)
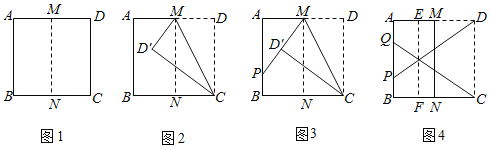
操作一:如图1,将正方形纸片ABCD对折,使点A与点D重合,点B与点C重合,再将正方形纸片ABCD展开,得到折痕MN;
操作二:如图2,将正方形纸片ABCD的右上角沿MC折叠,得到点D的对应的点为D′;
操作三:如图3,将正方形纸片ABCD的左上角沿MD′折叠再展开,折痕MD′与边AB交于点P;
(问题解决)
请在图3中解决下列问题:
(1)求证:BP=D′P;
(2)AP:BP= ;
(拓展探究)
(3)在图3的基础上,将正方形纸片ABCD的左下角沿CD′折叠再展开,折痕CD′与边AB交于点Q.再将正方形纸片ABCD过点D′折叠,使点A落在AD边上,点B落在BC边上,然后再将正方形纸片ABCD展开,折痕EF与边AD交于点E,与边BC交于点F,如图4.试探究:点Q与点E分别是边AB,AD的几等分点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com