
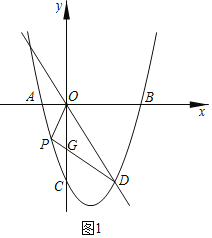
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

【答案】(1)抛物线的表达式为:![]() ;(2)
;(2)![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;(3)
;(3) ![]() 或
或![]() 或
或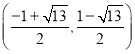 或
或 .
.
【解析】
(1)函数的表达式为:y=a(x+1)(x-3),将点D坐标代入上式,即可求解;
(2)设点![]() ,求出
,求出![]() ,根据
,根据![]()
![]()
![]() ,利用二次函数的性质即可求解;
,利用二次函数的性质即可求解;
(3)分∠ACB=∠BOQ、∠BAC=∠BOQ,两种情况分别求解,通过角的关系,确定直线OQ倾斜角,进而求解.
解:(1)函数的表达式为:![]() ,将点D坐标代入上式并解得:
,将点D坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() …①;
…①;
(2)设直线PD与y轴交于点G,设点![]() ,
,
将点P、D的坐标代入一次函数表达式:![]() 并解得,直线PD的表达式为:
并解得,直线PD的表达式为:![]() ,则
,则![]() ,
,
![]()
![]()
![]() ,
,
∵![]() ,故
,故![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;
;
(3)∵![]() ,∴
,∴![]() ,
,
∵![]() ,故
,故![]() 与
与![]() 相似时,分为两种情况:
相似时,分为两种情况:
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
过点A作AH⊥BC与点H,

![]() ,解得:
,解得:![]() ,
,
∴CH=![]()
则![]() ,
,
则直线OQ的表达式为:![]() …②,
…②,
联立①②并解得:![]() ,
,
故点![]() 或
或![]() ;
;
②![]() 时,
时,
![]() ,
,
则直线OQ的表达式为:![]() …③,
…③,
联立①③并解得:![]() ,
,
故点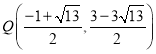 或
或 ;
;
综上,点![]() 或
或![]() 或
或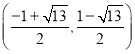 或
或 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中![]() 为下水管道口直径,
为下水管道口直径,![]() 为可绕转轴
为可绕转轴![]() 自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径
自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径![]() ,
,![]() 为检修时阀门开启的位置,且
为检修时阀门开启的位置,且![]() .
.
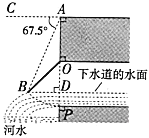
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中![]() 的取值范围;
的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达![]() 位置时,在点
位置时,在点![]() 处测得俯角
处测得俯角![]() ,若此时点
,若此时点![]() 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
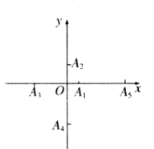
【题目】如图,在直角坐标系的坐标轴上按如下规律取点:![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() 在
在![]() 轴正半轴上,......,且
轴正半轴上,......,且![]()
![]() ......,设
......,设![]() ......,有坐标分别为
......,有坐标分别为![]() ,
,![]() ......,
......,![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,直接写出用含
时,直接写出用含![]() 为正整数)的式子表示
为正整数)的式子表示![]() 轴负半轴上所取点.
轴负半轴上所取点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月15日傍晚法国地标性建筑巴黎圣母院突遭大火吞噬,导致屋顶和主尖塔坍塌,哥特式的玫瑰花窗损毁.为了重建巴黎圣母院,设计小组设计了一个由三色玻璃拼成的花窗,如图所示,主体部分由矩形![]() 和半圆
和半圆![]() 组成,设半圆
组成,设半圆![]() 为区域
为区域![]() ,四个全等的直角三角形
,四个全等的直角三角形![]() 为区域
为区域![]() ,矩形内的阴影部分为区域
,矩形内的阴影部分为区域![]() ,其中
,其中![]() ,设
,设![]()
![]() 当
当![]() ,求区域
,求区域![]() 的面积.
的面积.
![]() 请用
请用![]() 的代数式表示出区域
的代数式表示出区域![]() 的面积并求出其最大值.
的面积并求出其最大值.
![]() 为了美观,设置区域
为了美观,设置区域![]() 与区域
与区域![]() 的面积之比为
的面积之比为![]() .区域
.区域![]() 、区域
、区域![]() 、区域
、区域![]() 分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为
分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为![]() 元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了
元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了![]() 元,求这三种玻璃的单价.(
元,求这三种玻璃的单价.(![]() 取
取![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
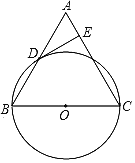
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为10,tanB=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与y轴交于点C.
(1)试用含m的代数式表示抛物线的顶点坐标;
(2)将抛物线y=x2﹣2mx+m2﹣1沿直线y=﹣1翻折,得到的新抛物线与y轴交于点D,若m>0,CD=8,求m的值.
(3)已知A(﹣k+4,1),B(1,k﹣2),在(2)的条件下,当线段AB与抛物线y=x2﹣2mx+m2﹣1只有一个公共点时,请求出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
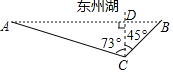
【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com