
【题目】2019年4月15日傍晚法国地标性建筑巴黎圣母院突遭大火吞噬,导致屋顶和主尖塔坍塌,哥特式的玫瑰花窗损毁.为了重建巴黎圣母院,设计小组设计了一个由三色玻璃拼成的花窗,如图所示,主体部分由矩形![]() 和半圆
和半圆![]() 组成,设半圆
组成,设半圆![]() 为区域
为区域![]() ,四个全等的直角三角形
,四个全等的直角三角形![]() 为区域
为区域![]() ,矩形内的阴影部分为区域
,矩形内的阴影部分为区域![]() ,其中
,其中![]() ,设
,设![]()
![]() 当
当![]() ,求区域
,求区域![]() 的面积.
的面积.
![]() 请用
请用![]() 的代数式表示出区域
的代数式表示出区域![]() 的面积并求出其最大值.
的面积并求出其最大值.
![]() 为了美观,设置区域
为了美观,设置区域![]() 与区域
与区域![]() 的面积之比为
的面积之比为![]() .区域
.区域![]() 、区域
、区域![]() 、区域
、区域![]() 分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为
分别镶嵌红、蓝、黄色三种玻璃,已知这三种玻璃的单价之和为![]() 元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了
元(三种玻璃的单价均为整数),整个花窗镶嵌玻璃共花费了![]() 元,求这三种玻璃的单价.(
元,求这三种玻璃的单价.(![]() 取
取![]() )
)

【答案】(1)12;(2)![]() ;
;![]() (3)红色玻璃单价为80元/m2,蓝色玻璃单价为49元/m2,黄色玻璃单价为61元/m2
(3)红色玻璃单价为80元/m2,蓝色玻璃单价为49元/m2,黄色玻璃单价为61元/m2
【解析】
(1)先求得一个直角三角形的面积,再乘以![]() 即可得区域
即可得区域![]() 的面积;
的面积;
(2)根据题意列出![]() 与
与![]() 的二次函数关系式,根据顶点式的系数特点得到其图象性质---开口方向以及增减性,再根据自变量
的二次函数关系式,根据顶点式的系数特点得到其图象性质---开口方向以及增减性,再根据自变量![]() 的取值范围,即可求得答案;
的取值范围,即可求得答案;
(3)设红、蓝、黄三种玻璃的单价分别为每平方米![]() 、
、![]() 、
、![]() 元,列出关于
元,列出关于![]() 、
、![]() 的二元一次方程,解出方程的正整数解即可得到答案.
的二元一次方程,解出方程的正整数解即可得到答案.
解:(1)根据题意可得:![]() ;
;
(2)∵由(1)可得:![]()
∴![]()
∴抛物线开口向下
∵对称轴为![]()
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
∵![]()
∴当![]() 时,
时,![]() ;
;
(3)设红、蓝、黄三种玻璃的单价分别为每平方米![]() 、
、![]() 、
、![]() 元
元
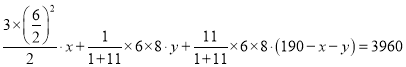
![]()
![]()
∵![]() 、
、![]() 均为正整数
均为正整数
∴![]() ,
,![]() ,
,![]()
答:红、蓝、黄三种玻璃的单价分别为每平方米![]() 元、
元、![]() 元、
元、![]() 元.
元.
故答案是:(1)![]() (2)
(2)![]() ;
;![]() (3)红色玻璃单价为80元/m2,蓝色玻璃单价为49元/m2,黄色玻璃单价为61元/m2
(3)红色玻璃单价为80元/m2,蓝色玻璃单价为49元/m2,黄色玻璃单价为61元/m2


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是( )

A. CE=![]() B. EF=
B. EF=![]() C. cos∠CEP=
C. cos∠CEP=![]() D. HF2=EFCF
D. HF2=EFCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”![]() 根据图表中提供的信息,回答下列问题:
根据图表中提供的信息,回答下列问题:

成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 |
|
(1)测试学生中,成绩为80分的学生人数有___名;众数是___分;中位数是___分;
![]() 若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有多少名?
若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
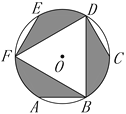
【题目】如图所示是一个圆形飞镖靶的示意图,其中A,B,C,D,E,F是⊙O的六等分点,如果向该飞镖靶上任意投一枚飞镖,则飞镖落在阴影区域的概率是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
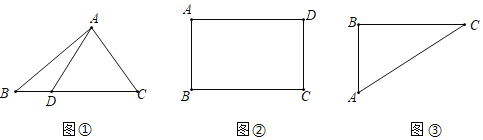
【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com