
分析 (1)①因为[x]=3,根据n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$,求得x取值范围即可;
②由①得出3x+1的取值范围,进一步解不等式组得出答案即可;
(2)设$\frac{5}{3}$x-1=m,m为整数,表示出x,进一步得出不等式组得出答案即可.
解答 题:(1)①$\frac{5}{2}$≤x$<\frac{7}{2}$;
②$\frac{1}{2}$≤x$<\frac{5}{6}$;
(2)设$\frac{5}{3}$x-1=m,m为整数,则x=$\frac{3m+3}{5}$,
∴[x]=[$\frac{3m+3}{5}$]=m,
∴m-$\frac{1}{2}$≤$\frac{3m+3}{5}$<m+$\frac{1}{2}$
∴$\frac{1}{4}$<m≤$\frac{11}{4}$,
∵m为整数,
∴m=1,或m=2,
∴x=$\frac{6}{5}$或x=$\frac{9}{5}$.
点评 本题考查理解题意的能力,关键是看到所得值是个位数四舍五入后的值,问题得解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
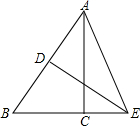 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )| A. | $\frac{7}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
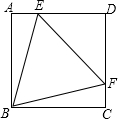 如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
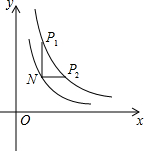 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或8 | C. | 2或6 | D. | 2或8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com