
【题目】如图,一个斜边长为10cm的红色三角形纸片,一个斜边长为6cm的蓝色三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红、蓝两张纸片的面积之和是( )
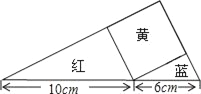
A. 60cm2 B. 50cm2 C. 40cm2 D. 30cm2
【答案】D
【解析】分析:标注字母,根据两直线平行,同位角相等可得∠B=∠AED,然后求出△ADE和△EFB相似,根据相似三角形对应边成比例求出![]() ,即
,即![]() ,设BF=3a,表示出EF=5a,再表示出BC、AC,利用勾股定理列出方程求出a的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
,设BF=3a,表示出EF=5a,再表示出BC、AC,利用勾股定理列出方程求出a的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
如图,∵正方形的边DE∥CF,
∴∠B=∠AED,
∵∠ADE=∠EFB=90°,
∴△ADE∽△EFB,
∴![]() ,
,
∴![]() ,
,
设BF=3a,则EF=5a,
∴BC=3a+5a=8a,
AC=8a×![]() =
=![]() a,
a,
在Rt△ABC中,AC2+BC2=AB2,
即(![]() a)2+(8a)2=(10+6)2,
a)2+(8a)2=(10+6)2,
解得a2=![]() ,
,
红、蓝两张纸片的面积之和=![]() ×
×![]() a×8a-(5a)2,
a×8a-(5a)2,
=![]() a2-25a2,
a2-25a2,
=![]() a2,
a2,
=![]() ×
×![]() ,
,
=30cm2.
故选D.


科目:初中数学 来源: 题型:
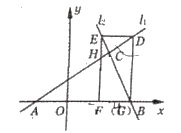
【题目】如图,已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 相交于点
相交于点![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,矩形
两点,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与
与![]() 点重合,那么
点重合,那么![]() __________________.
__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中如图,∠A=∠B=90°,将△AED、△DCF分别沿着DE、DF翻折,点A、C都分别与EF上的点G重合.
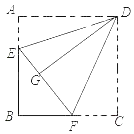
(1)求证:四边形ABCD是正方形;(2)若AB=6,点F是BC的中点,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若sinA=![]() ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )

A. 24m B. 22m C. 20m D. 18m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格当中,三角形![]() 的三个顶点都在格点上.直线
的三个顶点都在格点上.直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
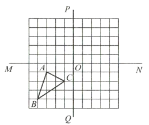
(1)画出将三角形![]() 向右平移5个单位长度后的三角形
向右平移5个单位长度后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(2)画出三角形![]() 关于直线
关于直线![]() 对称的三角形
对称的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(3)画出将三角形![]() 绕着点
绕着点![]() 旋转
旋转![]() 后的三角形
后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(4)在三角形![]() ,
,![]() ,
,![]() 中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读某同学解下面分式方程的具体过程.
解方程:![]() .
.
解:![]() ,①
,①
![]() ,②
,②
![]() ,③
,③
∴![]() .④
.④
∴![]() .
.
把![]() 代入原方程检验知
代入原方程检验知![]() 是原方程的解.
是原方程的解.
请你回答:
(1)上述解答正确吗?如果不正确,从哪一步开始出现错误?答:______.错误的原因是______(若第一格回答“正确”的,此空不填).
(2)给出正确答案(不要求重新解答,只需把你认为应改正的进行修改或加上即可).___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
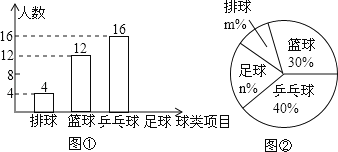
(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com