练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】请阅读某同学解下面分式方程的具体过程.

    解方程：．

    解：，①

    ，②

    ，③

    ∴．④

    ∴．

    把代入原方程检验知是原方程的解.

    请你回答：

    （1）上述解答正确吗？如果不正确，从哪一步开始出现错误？答：______．错误的原因是______（若第一格回答“正确”的，此空不填）．

    （2）给出正确答案（不要求重新解答，只需把你认为应改正的进行修改或加上即可）.___________

    【答案】错误从第③步开始错误， 分子﹣2x+10可能为0． 或，得或.

    【解析】

    （1）第③步没有讨论﹣2x+10是否等于0，故错误；

    （2）增加﹣2x+10=0的情况，解答即可．

    （1）有错误．从第③步出现错误，原因：分子﹣2x+10可能为零；

    （2）或，解得：或．

    经检验：x=5，都是原方程的解，

    故原方程的解为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（2011贵州安顺，17，4分）已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为 ．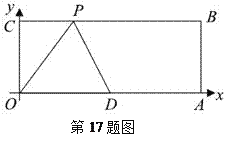

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．

    （1）用含x的代数式表示线段CF的长；

    （2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设=y，求y关于x的函数关系式，并写出它的定义域；

    （3）当∠ABE的正切值是时，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个斜边长为10cm的红色三角形纸片，一个斜边长为6cm的蓝色三角形纸片，一张黄色的正方形纸片，拼成一个直角三角形，则红、蓝两张纸片的面积之和是（　　）

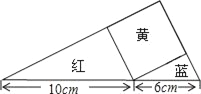
    A. 60cm2 B. 50cm2 C. 40cm2 D. 30cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一矩形纸片放在直角坐标系中，为原点，点在轴上，点在轴上，.

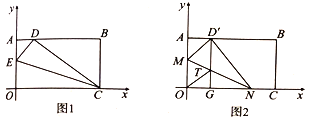
    （1）如图1，在上取一点，将沿折叠，使点落在边上的点处，求直线的解析式；

    （2）如图2，在边上选取适当的点，将沿折叠，使点落在边上的点处，过作于点，交于点，连接，判断四边形的形状，并说明理由；

    （3）、在（2）的条件下，若点坐标，点在直线上，问坐标轴上是否存在点，使以为顶点的四边形是平行四边形，若存在，请直接写出点坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用勾股定理可以在数轴上画出表示的点，请依据以下思路完成画图，并保留画图痕迹：

    第一步：（计算）尝试满足，使其中a，b都为正整数.你取的正整数a=____，b=________；

    第二步：（画长为的线段）以第一步中你所取的正整数a，b为两条直角边长画Rt△OEF，使O为原点，点E落在数轴的正半轴上， ，则斜边OF的长即为.

    请在下面的数轴上画图：（第二步不要求尺规作图，不要求写画法）

    第三步：（画表示的点）在下面的数轴上画出表示的点M，并描述第三步的画图步骤：_______________________________________________________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学决定派3名教师带领名学生到北京参加夏令营活动，甲旅行社的收费标准为：教师全价，学生半价优惠；乙旅行社的收费标准为：教师和学生全部按全票价的6折(即全票价的60％)优惠．已知甲、乙两家旅行社的全票价均为240元．试解答下列问题：

    (1)用代数式表示甲、乙两家旅行社的收费各是多少元？

    (2)当时，如果你是校长，你会选择哪一家旅行社？并简单说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个长方形运动场被分隔成、、、、共个区， 区是边长为的正方形， 区是边长为的正方形．

    （1）列式表示每个区长方形场地的周长，并将式子化简；

    （2）列式表示整个长方形运动场的周长，并将式子化简；

    （3）如果， ，求整个长方形运动场的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣ ），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．

    （1）求A、B两点的坐标；

    （2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

    （3）当△BDM为直角三角形时，求m的值．

    查看答案和解析>>

    同步练习册答案