
分析 (1)根据循环节”的数字个数叫做循环节的阶数,可得答案;
(2)根据一个能被9整除的2阶4位循环数,可得$\frac{2(a+b)}{9}$,根据不等式的性质,可得答案.
解答 解:(1)1717是2阶4位循环数,7171是2阶4位循环数;
证明:设原数为$\overline{abab}$,新数为$\overline{baba}$
即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
1000b+100a+10b+a-(1000a+100b+10a+b)
=990b-909a
=909(b-a)
=9×101(b-a),
∵a,b为整数,
∴b-a也为整数,
∴新数和原数的差能够被9整除;
(2)该2阶4位循环数为 $\overline{abab}$,
即$\frac{1010a+101b}{9}$
=112a+11b+$\frac{2(a+b)}{9}$,
要使得1010a+101b能被9整除,则需(a+b)能被9整除,
∵0<a≤9,0<b≤9,
∴0<a+b≤18,
∴a,b应满足的关系是a+b=9或a+b=18.
点评 本题考查了因式分解的应用,理解循环阶的阶数是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
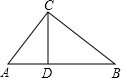 红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
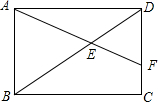 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com